[분류 전체보기]검색결과, 375건
- 프로덕트 리더가 반드시 피해야 할 5가지 실수 2023.10.10
- 실수 연산, 어떻게 하시나요??? 2023.09.27 3
- +- m * n의 e승 2023.09.27 1
- 실수 데이터의 표현 방식 - 부동소수점 방식 2023.09.27 2
- 0.1 을 100 번 더해도 10이 되지 않는다? 2023.09.27 2
- 정수 데이터의 표현 방식 2023.09.27 2
- 2진수 <-> 8 진수, 16 진수 변환 2023.09.27 2
- n 진수? 진수 변환 ! 2023.09.27
- 다시 블로그 2023.09.27 2
- 성공한 후... 2022.07.13 2
- 기술사 면접 질문(2016년 4월 그때...) 2022.02.21 2
- 개인정보의 암호화 대상 및 방법 2020.07.28 1
- 내가 취득한 자격증과 인증 2020.06.03 2
- 감사하며 살기 2020.05.12
- Core/Context 모델 2019.03.20
오랜만에 공감가는 읽을거리 하나 공유 합니다.
오전에 출근해서 메일링으로 온 것인데, 프로젝트를 리딩하는 입장에서 도음이 될 만한 내용이네요.
프로덕트 리더가 반드시 피해야 할 5가지 실수
프로덕트 리더가 반드시 피해야 할 5가지 실수
오늘은 프로덕트 리더가 범하기 쉬운 5가지 실수들에 대해 알아보고, 배달의 민족과 카카오를 거쳐 지금은 개발 이사로 일하고 있는 손현태 리더님의 인사이트까지 함께 확인해 보겠습니다.
www.grownbetter.com
특히 2번 내용에 적잖이 공감을 하는데...
2. 품질보다 양을 우선시한다.
빠른 성장을 추구하다 보면 제품 로드맵에 수많은 기능들을 가득 채우고 싶은 유혹에 빠지기 쉽습니다. 하지만 한 번에 모든 것을 처리하려고 하면 집중력이 흐려지고 팀에 부담을 줄 수 있습니다.
정확하고 단호하게 우선순위를 정하여 이러한 실수를 피하세요. 그리고 제품의 핵심 가치 제안에 집중하여 각 기능이 중요한 목표에 부합하는지 확인하세요. 변화하는 시장 상황과 사용자 피드백에 적응하기 위해 로드맵을 지속해서 검토하고 조정하는 것도 잊어서는 안 됩니다.
개인적으로 같은 맥락에서 조금 덧 붙이고 싶은 내용이 있다.
개발 스펙을 잡을 때,
무엇을 개발할 것인가? 를 정의하는 것 못지않게 중요한 것이 무엇을 개발하지 않을 것인가? 를 정의하는 것도 아주 중요하다.
소프트웨어 개발 현장에서 자주 목격되는 현상이다.
비즈니스의 전략과 그 전략을 실현하기 위한 본질만을 기능으로 정의(스펙인)하는 것을 넘어, 자기 자신이 이 기능에 대해 깊고 다양하게 생각할 수 있음을 피력하는 수단으로 스펙을 정의하는 실수말이다.
사실 이런 것들 중 대부분은 치장하기 기능으로 스펙아웃의 대상이 되어야 하거나 지금 당장은 필요치 않은 부가기능(핵심 기능을 런칭한 후 개발해도 되는 기능)들이 대부분이다. 즉 오버스펙이거나 좋은 기능이지만 지금 당장은 필요하지 않은 기능!
특히 스타트업은 시간과 자원이 한정되어 있다.
본질적인 기능을 시장에 빠르게 런칭하고 데이터와 고객의 반응을 보면서 점진적으로 개선해 나가는 것이 중요하다고 생각한다.
국제적인 프로젝트 관리 협회인 PMI는 프로젝트의 3대 제약사항을 '일정/원가/범위'로 정의했다.
앞서 언급한 치장하기 기능들은 이 3가지 요소 모두에 영향을 미친다.
더불어 프로덕트의 품질에도 영향을 미친다. 더 많은 기능은 필연적으롸 더 많은 검증이 필요하고 더 많은 버그 가능성을 내포한다.
이것은 린스타트업, 린소프트웨어개발방법론의 철학에도 깔려 있는 원칙이다.
린 방법론의 핵심은 생산에 있어 낭비요소를 제거(or 최소화)하는 것이다.
소프트웨어 개발과정에서 불필요한 기능, 오버 스펙된 기능, 나중에 필요한 기능 등은 모두 (현재 시점에서는) 낭비요소이다.
핵심 기능만을 오류 없이 고품질로 런칭하여 프로덕트의 성장성과 기회를 빠르게 증명하는 것이 무엇보다 중요하다고 생각한다.
린 방법론에 대해서는 아래의 글이 핵심을 잘 정리해 놓은 듯 하니, 참고하면 좋겠다.
https://brunch.co.kr/@kbhpmp/22
'일상' 카테고리의 다른 글
| 금연 꿀팁(흡연의 욕구를 단박에 떨쳐버리기) (0) | 2023.10.26 |
|---|---|
| 다시 블로그 (2) | 2023.09.27 |
| 성공한 후... (2) | 2022.07.13 |
| 기술사 면접 질문(2016년 4월 그때...) (2) | 2022.02.21 |
| 내가 취득한 자격증과 인증 (2) | 2020.06.03 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=530
---
(이 글은 닷넷 프레임워크 기반의 예제 및 개념입니다. 그러나 대부분의 개념은 언어와 무관합니다)
여러분들은 '실수 연산'을 할 일이 있나요?
간혹, 랜덤한 값을 계산하거나, 그래프를 그릴 때, 간혹 실수 연산을 할 일이 있을 겁니다
그러나 이 경우에는 정확한 결과가 나오지 않아도 되는 경우가 많습니다
따라서 질문을 다시 해 보죠
여러분들은 정확한 실수 연산을 할 일이 있나요?
다음의 코드의 실행 결과를 예상해 보세요
double a = 11.22;
double b = 11.10 + 0.12;
bool result = (a == b);
result 는'참' 일까요, '거짓' 일까요?
인간의 계산(?) 방식대로 하면, 11.10 + 0.12 = 11.22 이기 때문에 a, b 두 값은 같으니까, 결과는 '참' 이어야 겠죠
그러나 결과는 '거짓' 입니다
컴퓨터는 인간처럼 계산하지 않는다는 게 원인이죠
이와 관련해서 자세한 내용은, 다음의 제 글들을 확인해 주세요
-> 0.1 을 100 번 더해도 10이 되지 않는다?
-> 실수 데이터의 표현 방식 - 부동소수점 방식
-> +- m * ne
그러면, 위 코드에 의해, 컴퓨터가 계산한 결과를 볼까요?
실수의 부동소수점 표현을 보기 위해 C# 에서 Console.WriteLine 에 형식 문자열(E/e)로 16자리까지 봅시다
double a = 11.22;
double b = 11.10 + 0.12;
Console.WriteLine("{0:e16}", a);
Console.WriteLine("{0:e16}", b);

어떻습니까?
두 값은 엄연히 다릅니다. 이것이 바로 컴퓨터가 계산한 결과 입니다
위에 제시한 링크의 글들을 보셨다면 이유는 아셧을 겁니다
컴퓨터가 실수를 표현하는 부동소수점 방식은 특정한 식에 의해 최대한의 근사치 만을 표현하기 때문입니다
---------------------------------------------------------------------------------------------------
참고로, 우리나라 화폐단위는 (간편하게도) 소수점이 없죠.
미국 화폐의 경우 센트 단위가 있어, 화폐 계산 할 때 소수점 연산이 필요한 경우가 있습니다
돈이 걸린 문제는 민감하죠. 그래서 돈 계산에 실수가 사용된다면 정확한 결과를 보장해야 겠지요
그런데, 문제는 실수 연산은 정확하지 않다는 겁니다
더 정확하게 말하자면, 부동소수점 방식의 실수 연산을 정확하지 않다는 거죠
만일, 돈 계산과 같이, 실수 연산이 매우 정확해야 한다면 부동 소수점을 사용하면 안됩니다
대표적인 부동 소수점 데이터타입으로는 float(single) 과 double 이 있죠
즉 실수를 double 로 선언해서 돈 계산을 하면 안된다는 말입니다
가장 간편한(?) 방법은 decimal 데이터 타입을 사용하는 것이죠
msdn의 다음문구를 참고하세요
'Single 및 Double에서는 정확하지 않는 숫자가 Decimal에서는 정확하게 표시되는 경우가 있습니다(예: 0.2, 0.3).
Decimal에서는 부동 소수점에서보다 산술 연산이 더 느리지만 더 정확한 결과가 나타나므로 성능 감소를 감내할
만한 가치가 있습니다'
그리고 중요한 것은 현재 환경에 맞는 최적의 선택이죠. msdn은 이렇게 권고합니다
'Decimal 데이터 형식은 모든 숫자 형식 중 가장 느린 형식입니다. 데이터 형식을 선택하기 전에 정밀도와 성능 중
무엇이 더 중요한지를 충분히 검토해야 합니다'
따라서, (실수가 포함된) 회계계산에는 언어를 불문하고 decimal 을 많이 사용합니다
(한국 화폐 기준만 사용하시나요? 그렇다면, int64 로도 충분할 것입니다)
앞서 예제 코드를 double 대신 decimal 로 바꿔 봅시다
decimal a = (decimal) 11.22;
decimal b = (decimal)11.10 + (decimal)0.12;
bool result = (a == b);
Console.WriteLine(result.ToString());
Console.WriteLine("{0:e16}", a);
Console.WriteLine("{0:e16}", b);
결과입니다

값이 같다는 결과를 보여주죠..
이제, 이 글에서 제가 하고 싶은 본론입니다
decimal 을 사용하지 않고도 실수 연산의 결과가 보장(?)되어야 한다는 경우가 있을 것입니다
음.. 사실 이 표현은 정확하지 않죠. 부동소수점 연산 자체가 이미 정확하지 않은데 어떻게 연산의 결과를
보장하겠습니까?
그러면 표현을 다르게 해 보죠
부동소수점 실수를 사용하고도 허용하는 범위 내에서는 결과가 (오차가 없다는 것을) 보장해야 한다
이러면 말이 되죠. 이러한 것을 내결함성 허용이라 합니다
부동소수점 실수 연산에서 연산의 결과가 차이나는 것은 컴퓨터의 실수 표현에 따른 미세한 오차 때문입니다
즉 이러한 미세한 차이는 허용할 수 있다는 가정입니다. 대부분은 이러한 미세한 차이는 허용가능합니다
잘 생각해 보세요. 0.1%의 오차도 허용하지 않겠다.... 라고 한다면 부동소수점 사용하면 안됩니다
실수 연산이 돈 계산만 아니면 (경우에 따라서는 돈 계산이라 할지라도),
어느 정도의 오차는 허용가능한 경우가 대부분입니다
0.1%의 오차 허용이 수치로 와 닿지 않나요?
그러면 특정 소수점 자리 수 까지만 정확성을 보장하면 되나요?
그렇다면, 부동 소수점으로도 충분히 연산 가능합니다
아래 코드는 0.%의 오차를 허용하는 환경에서의 두 값 비교 입니다
double a = 11.22;
double b = 11.10 + 0.12;
double difference = a * 0.0001; //0.1% 오차는 허용함
bool result = Math.Abs(a - b) <= difference; // true 반환
부동소수점 연산 결과의 오차는 특정한 범위 내에서는 허용가능한 경우가 많습니다
즉 컴퓨터가 부동소수점을 표현하는 방식에시 기인한 오차 범위 수준 정도는 무시해도 된다는 거죠
예를 들어, 소수점 2자리 까지만 사용하는 환경에서
0.0000001 오차 때문에 double 대신 decimal 을 사용한다는 것은 좀 오버 아닐까요???
MS 고객지원 사이트에는 다음과 같은 글이 있습니다
'서로 같은지 확인하기 위해 두 개의 부동 소수점 값을 비교하지는 마십시오.
반드시" 같아야 하는 두 숫자 사이에도 항상 약간의 차이가 납니다.
그 대신 항상 숫자들이 거의 근사한 값인지 확인하십시오.
즉, 두 수의 차이가 아주 작은지 또는 무의미한지 확인하십시오'
다음의 MS 자료들을 찬찬히 읽어 보시길 권장 드립니다
http://support.microsoft.com/kb/42980/ko
http://support.microsoft.com/kb/125056/ko
http://support.microsoft.com/kb/69333/ko
http://msdn.microsoft.com/ko-kr/library/c151dt3s.aspx
'SW개발' 카테고리의 다른 글
| ASCII (249) | 2023.10.27 |
|---|---|
| 비트(bit) 단위 연산 (0) | 2023.10.27 |
| +- m * n의 e승 (1) | 2023.09.27 |
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=99
---
앞에서 부동 소수점 방식에 대해 간략히 알아 봤습니다. 보통 프로그래밍 언어에서 실수형 데이터를 저장하기 위해
두가지 데이터 타입을 둡니다. float 와 double 이지요..
float : 단정도 부동 소수 (32비트)
double : 배정도 부동 소수 (64비트)
데이터를 표현하는데 사용되는 비트수가 다르기 때문에 당연히 표현가능한 수의 범위가 달라집니다.
컴퓨터는 실수형 데이터를 표현하기 위해 할당되어진 비트들 중 특정 비트를 지수,가수,부호로 사용함으로써
실수를 표현합니다. 이 두 형식 모두 앞서 살펴본 (아래의)부동 소수 표현식으로 표현됩니다.
+- m * n의 e승
+- : 부호
m : 가수
n : 기수
e : 지수
아래의 그림은 배,단정도 부동소수 저장시 사용되어 지는 메모리 구조 입니다.
1) 단정도 부동 소수의 메모리 구조(32 비트 사용)

2) 배정도 부동 소수의 메모리 구조(64 비트 사용)

앞서, 우리는 위 표현식이 엄밀히 말하면 아래와 같다고 했습니다.
+- 1.m * 2의 e-127승
이유를 하나하나 살펴 봅니다.
[1] 기수는 2 이다
컴퓨터는 2진수를 사용하기 때문에 기수는 2가 되어 아래의 표현식으로 됩니다
+- m * 2의 e승
[2] 지수부는 excess 표현이 사용된다
지수부 역시 양수와 음수를 가져야 합니다.
10진수의 부동소수 표현에서 10의 지수 값으로 소수점의 위치가 변동 됨을 알 수 있습니다. 이는 2진수도 마찬가지
입니다. 즉, 지수부의 값이 - (마이너스) 가 되어야 할 필요가 있다는 말입니다. 그러나 지수부를 위한 메모리 공간에
는 별도의 부호 비트는 없습니다. 따라서 특별한 규칙을 만들어 마이너스를 표현하는데요...
이때 사용되는 것이 excess 표현입니다.
excess 표현은 지수부에서 나타낼 수 있는 최대 값을 반으로 나누어 그 값을 0 으로 보고
그것(0)보다 큰 값을 양수처럼, 작은값을 음수로 계산하는 것입니다.
(즉 최대값을 반으로 나눈 값을 기준으로 본다는 말이 됩니다)
한가지 예를 들어 보겠습니다.
단정도 부동소수인 float 에서 지수부를 위한 메모리 공간은 8비트 입니다.
8비트로 표현할 수 있는 최대 수는 11111111 이므로 10진수로 255 가 됩니다.
255 / 2 = 127.5 가 됩니다. 여기서 소수점 0.5는 버립니다.
즉 127을 0으로 취급합니다.
이때 지수부의 실제 값이 128이면 excess표현으로 인한 지수의 값은 1 이 되는 셈입니다
따라서 지수부의 값은 e-127 이 되느 것입니다.
+- m * 2의 e-127승
[3] 가수부는 특정 규칙을 사용하는 정규 표현을 사용한다
부동소수는 이미 알아본 바와 같이 다양한 형태로 표현될 수 있습니다.
10진수로 예를 들면 고정 소수 0.12 를 표현하기 위한 부동 소수는 아래와 같이 다양합니다.
0.12 = 0.12 * 10의 0승
0.12 = 12 * 10의 -2승
0.12 = 0.012 * 10의 1승
이와 같이 같은 수에 대한 표현방법이 다양하다면, 컴퓨터로 처리하기가 어려워 집니다. 따라서 특정한 표현방식
하나만 정해서 사용합니다. 위의 0.12 를 아래와 같이 하나의 표현 방식만 사용한다고 정해 둔다는 것입니다.
'소수점 이상은 0으로 하고, 소수점 이하 첫번째 자리는 0이 아닌 값으로 한다'
위의 규칙대로라면 0.12의 부동 소수 표현은 0.12 = 12 * 10의-2승 .. 이것만 가능 합니다.
이와 같이 특정 규칙을 정해 그 규칙대로만 표현하는 것을 정규 표현이라 합니다. 컴퓨터에서 2진수로 표현하는 부동소수 표현 방식에 이와 같은 규칙이 있습니다. '소수점 이상을 1로 고정한다' 라는 정규 표현을 사용합니다.
즉 반드시 정수부의 첫번째 자리는 1로 만들고 그 이상의 자리는 0으로 해주는 표현방법입니다.
소수점 이상을 1로 고정 하기 위해 2진수의 쉬프트 연산이 일어납니다. 또한 이렇게 고정한 1은 가수부의 표현
비트내에 포함시키지 않습니다. 정수부의 첫번째 자리는 반드시 1이라고 규칙을 정해 놓았기 때문에 별도의
비트가 필요치 않으며 가수부 비트내에 포함시키기 않음으로써 조금 더 넓은 범위의 수를 표현할 수 있게 됩니다.
(단정도 부동소수의 경우 23비트로 가수부를 표현하는데 첫번째 자리 1이 생략되었다고 할 수 있으므로 총 24비트
를 사용한다고 할 수 있을 것입니다)

아래는 단정도 부동 소수에서 가수부의 정규 표현을 사용하여 표현한 것입니다.
1011.0011 <- 원래의 숫자
0001.0110011 <- 정수부의 첫번째 자리가 1이 되도록 오른쪽 쉬프트
0001.01100110000000000000000 <- 소수점 이하를 23비트로 만듦
01100110000000000000000 <- 소수점 이하만 뽑아 정규 표현을 완료
Example>>
2진수로 표현된 실수(단정도 부동소수)가 아래와 같다고 할때 10진수로 변환하면...?
0 01111110 10000000000000000000
부호 지수부 가수부
1) 부호비트가 0 이므로 양수입니다.
2) 지수부의 값이 126 이므로 (127 - 126) = -1 , 즉 2의 -1 승 , 0.5가 됩니다.
3) 가수부의 소수점 이상 첫번째 자리가 1이므로
위의 가수부의 값은 1.10000000000000000000000 이 됩니다.
즉 10진수로 1.5가 됩니다.
결론)
+- m * 2의 e승
이 표현식에 대입해 보면 + 1.5 * 0.5 = 0.75 가 됩니다
'SW개발' 카테고리의 다른 글
| 비트(bit) 단위 연산 (0) | 2023.10.27 |
|---|---|
| 실수 연산, 어떻게 하시나요??? (3) | 2023.09.27 |
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=98
---
컴퓨터가 정수를 표현하는 방식과 실수를 표현하는 방식은 크게 다릅니다.
실수 표현 방식을 이해하기 위해 아래와 같은 가정으로 출발하여 컴퓨터가 실수 표현을 하는 방식에 대해 알아
봅니다. 한가지 예를 들겠습니다.
만일 2바이트의 메모리로 실수를 표현한다고 가정할때, 가장 쉽게 생각해서 반을 나누어 1바이트에는 소수점
이상의 값을, 또 다른 1바이트에는 소수점 이하의 값을 저장한다고 칩시다. 아래와 같이 표현될 것입니다.
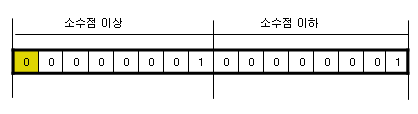
위와 같이 표현한다면 소수점 이상이 00000001 이므로 10진수 1이 되며, 소수점 이하는 00000001 이 되어 10진수
1이 되므로 +1.1 이 된다고 해석될 것입니다.
아주 심플하면서도 이해하기 쉽습니다. 그러나 컴퓨터는 일반적인 실수 표현을 위와 같은 방식을 채택하지는
않았습니다. 이유가 뭘까요?? (쉬운데 기냥 저렇게 하지-.-;)
이유는 바로 데이터의 표현한계입니다.
위와 같이 실수를 표현한다면 2바이트로 표현할 수 있는 실수의 범위는 아주 작습니다. 4바이트든, 8바이트든
실수 표현 범위의 한계를 가질 것입니다. 그렇다고 해서 아주 넓은 범위의 실수를 표현하기 위해 메모리를 확
늘려 데이터를 저장한다고 하면 해결책이 될까요?? 도대체 얼마나 많은 메모리를 요구해야 현실세계의 실수를
모두 표현 할 수 있을까요??
그래서 컴퓨터는 적은 수의 비트 수를 가지고 넓은 범위의 실수를 표현하기 위해서 하나의 식을 만들었습니다.
+- m * n의 e승
+- : 부호
m : 가수
n : 기수
e : 지수
위와 같은 식을 미리 정해 놓고 일부 비트는 가수로 일부 비트는 지수의 값을 정하는데 사용하여 실수를 표현합니다.
위의 식을 도입하여 적은 비트로 넓은 실수 범위를 표현가능 하다는 장점을 얻었지만 실수표현에서의 오차를 허용 할 수 밖에 없는 단점도 가지게 되었습니다. 앞서 살펴본 실수표현의 오차는 실제로 위의 식으로 기인하는 것입니다.
위와 같이 실수에서 소수점의 위치를 고정 시키는 것이 아니라 지수승에 따라 소수점이 움직일 수 있는 것을
부동 소수점 표현 방식이라고 합니다. (부동의 '부' 는 아닐 '부' 가 아닙니다. 둥둥 떠 다니는 '부' 입니다 ^^;)
위의 부동 소수의 표현 방식은 정확히 말해 아래와 같이 표현됩니다.
+- 1.m * 2의 e-127 승
즉 2진수에서 기수는 2이며 가수부와 정규표현과 지수부의 excess 표현이 사용된 것입니다.
이에 관해 다음에 자세히 알아 봅니다
참고>
우리가 사용하는 10진수에서도 고정,부동 소수점 표현방식으로 소수점을 표현을 달리 할 수 있습니다.
ex> 0.12 의 소수점을 가진 실수의 표현은 아래와 같이 다양합니다.
1)0.12 = 0.12 * 10의0승
2)0.12 = 12 * 10의-2승
3)0.12 = 0.012 * 10의1승
즉 고정소수점인 0.12 는 10의 지수승의 변화를 주어 다양한 부동 소수점 방식으로 표현 될 수 있습니다
'SW개발' 카테고리의 다른 글
| 실수 연산, 어떻게 하시나요??? (3) | 2023.09.27 |
|---|---|
| +- m * n의 e승 (1) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=97
---
너무나도 유명한 문구가 아닌가 싶습니다.
기초 C언어 공부할때나 프로그래밍 원리 같은 공부할때 꼭 등장하는 말입니다. 저도 그 말을 인용해 봤습니다.
이 말은 컴퓨터의 실수 표현 방식과 그에 따른 오차에 관한 말인데요.. 실제로 실수형 데이터의 연산에는 오차가
발생합니다. (직접해보세요.. 0.1 , 100 번 더하기)
이미 우리는 앞에 2진수로 표현된 수를 10진수로 변환하는 방법을 알고 있습니다. 그러면 2진수로 표현된 소수를
10진수로 변환하는 방법은요??? ... 마찬가지 입니다.
EX>2진수 1.01 을 10진수로 만들어 보겠습니다.
(2진수) 1.01 => 1*2의0승 + 0*2의-1승 + 1*2의-2승 = 1 + 0 + 0.25 = 1.25 (10진수)
이렇듯 2진수를 10진수로 표현할 때는 소수점을 기점으로 2의 (+,-)승을 해나가면 됩니다.
그렇다면 10진수 소수인 0.1 은 2진수로 어떻게 표현될까요???
소수점 이하 자리는 2의 마이너스 승이므로 2의 -1 승부터 차례로 해 보겠습니다
2의-1승 = 0.5 , 2의-2승 = 0.25 , 2의-3승 = 0.125 , 2의-4승 = 0.0625 ………
0.125 에서 바로 0.0625 로 넘어가 버렸습니다. 0.1은 나오지도 않았는데 말이죠..
물론 비트 자릿수를 늘려 이 들 숫자의 조합으로 0.1 에 가까운 수를 찾을 수는 있습니다만, 0.1이 아닌 근사값이
됩니다. 위의 산술과정은 비트자릿수를 하나씩 늘려서 0보다 큰 제일 작은 수를 나타낸 것인데요..
이런 방식이 아니더라도 소수점 이하 4비트를 가지는 메모리에서 표현되는 수를 다시 한번 보겠습니다.
소수점 이하 4비트를 가지는 2진수의 제일 작은 수 : 0.0000 => 10진수 0
소수점 이하 4비트를 가지는 2진수의 그 다음 작은 수 : 0.0001 => 10진수 0.0625
즉, 이 메모리로는 10진수 0과 0.0625 사이의 값은 표현할 수가 없습니다.
비트 수를 더 늘리면 더 좁은 간격의 수가 나올 수 는 있겠습니다만..
이렇듯 컴퓨터는 10진수 실수를 표현하는데 오차를 가집니다.
10진수에 해당하는 실수 값에 근사값을 나타낼 수 있을 뿐이지요..
결론적으로 0.1 이라는 값을 가지는 변수를 선언하면 그 변수에는 실제 0.1이 들어가는 것이 아니라 0.1의 근사값이
저장됩니다. 즉, 0.1의 근사값을 100번 더해봤지 10이 될리 없는 것입니다.
실제로 10진수 0.1을 2진수로 변환하면 0.00011001100....... (이하 1100 반복)이 됩니다
이런 수를 수학에서는 순환소수라 합니다.
대표적인 순환소수는 1/3 이 있습니다. 1/3 을 소수로 표현하면 0.33333.....(이하 3반복) 이 됩니다
참고>>
위의 내용은 문제를 간단하게 표현하기 위해 그리고 오차가 나는 이유를 이해하기 위해 2진수 소수 표현방식을 나타 냈습니다. 그러나 실제로 컴퓨터는 실수 표현을 단순히 소수점을 가진 2진수로 표현하지는 않습니다.
미리 말씀드리자면 일정한 식을 가지고 비트를 각 영역별로 나누어 저장,표현합니다. 이에 대해선 다음에 알아봅니다
'SW개발' 카테고리의 다른 글
| +- m * n의 e승 (1) | 2023.09.27 |
|---|---|
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
| n 진수? 진수 변환 ! (0) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=96
---
이제 컴퓨터가 정수 데이터를 표현하는 방식에 대해 알아 봅니다.
* 데이터
컴퓨터가 표현 하는 모든 데이터는 2진수로 표현되는 것을 알고 있습니다. 이때 데이터란 정수나 실수처럼 수 일수도 있고 문자, 사운드, 동영상 등 컴퓨터가 표현하는 모든 것을 의미 합니다. 현재 이렇게 글을 작성하고 있는 것도 우리들 눈에는 문자로 보이지만 컴퓨터는 1 과 0 의 조합으로 인식합니다.
* 데이터 표현 단위
컴퓨터가 데이터를 나타내는 최소 단위는 비트입니다. 이 비트는 0 과 1 중 한 값을 저장할 수 있는 메모리 공간입니다.
이 비트들이 모여 바이트를 이루며 바이트가 모여 Kbyte 가 되며 Mbyte, Gbyte, 가 됩니다.
8 bit -> 1 byte 입니다. 아래는 8 bit(1byte) 메모리에 숫자 7이 저장된 모습입니다

1 비트에는 0 또는 1 을 표현할 수 있습니다. 이 말은 1 비트로 표현 가능한 수가 최대 2가지란 말이 됩니다.
1 + 1 비트, 즉 2 비트가 표현 할 수 있는 최대 가지 수는 ( 2 * 2) = 4 가지가 됩니다. 이와 같이 N 비트로 표현
할 수 있는 최대 데이터 가지 수는 2의 n 개가 됨을 알 수 있습니다
참고로 비트는 정보를 표현하는 최소 단위라고 하며 바이트는 문자를 나타내는 최소 단위라고 합니다
* 컴퓨터의 정수 표현 방식
정수란 0을 포함한 음과 양의 소수가 아닌 수를 의미합니다.
1. 양의 정수 표현 방식
닷넷에서의 대표적인 정수는 short 와 int 가 있습니다. 각각 2byte, 4byte 로 정수를 저장합니다
단, 모든 수의 가장 왼쪽 비트는 부호 저장용으로 사용됩니다. 이를 부호 비트라 합니다 (0 : 양수 , 1: 음수)
이 부호 비트를 MSB(Most Significant Bit) 라고 합니다
아래는 short 형 수 15 가 저장된 메모리 구조입니다 ( 노란색 비트는 부호비트 입니다)

2. 음의 정수 표현 방식
음수를 표현 할 때는 단순히 부호비트만 변경하면 되는 것이 아닙니다. 수학적으로 음수는 양수의 반대되는 값 ,
즉 양수N + 음수N = 0 이 되면 음수가 되는 것입니다. 컴퓨터는 이런 음수를 양수의 2의 보수로 표현합니다.
(물론 음수의 2의 보수는 다시 양수가 됩니다) 2의 보수 구하는 식 => 1의 보수 구하기 + 1 더하기 위의 15의 2의
보수를 구해 보겠습니다

'SW개발' 카테고리의 다른 글
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
|---|---|
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
| n 진수? 진수 변환 ! (0) | 2023.09.27 |
| 개인정보의 암호화 대상 및 방법 (1) | 2020.07.28 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=100
---
앞서 10 진수를 기준으로 2,8,16 진수의 변환을 알아 보았습니다.
이번에는 2진수를 8진수와 16진수로 변환하는 방법과
8진수,16진수를 2진수로 변환하는 방법을 알아 봅니다.
1. 2진수를 16진수로 변환하기.
2진수로 데이터가 저장되는 정보의 최소 단위인 비트가 4개 모이면 16진수 한 자리에 해당됩니다.
즉, 아래와 같이 4비트에 메모리에 저장할 수 있는 최대값은 15 가(16진수 f) 됩니다
|
1
|
1
|
1
|
1
|
(1 * 2의3승) + (1 * 2의2승) + (1 * 2의1승) + (1 * 2의0승) = 15(10진수) = F(16진수)
따라서 2진수 4자리는 16진수 한자리에 해당되므로
아래와 같은 2진수를 16진수로 변환 할때는 4자리씩 끊어서 16진수 한자리로 변환하면 됩니다.
11011111 = 1101 1111 = DF 가 됩니다.
또한 4자리로 끊었을때 자리수가 부족하면 0으로 채워서 계산하면 됩니다.
1101111 = 0110 1111 = 6F 가 됩니다.
그리고 소수점을 포함한 2진수도 마찬가지 개념으로 변환하면 됩니다.
1011.011 = 1011 . 0110 = B.6 가 됩니다.
2. 2진수를 8진수로 변환하기
위의 개념과 완전 동일합니다.
2진수 비트 3개는 8진수 한자에 해당 됩니다.
|
1
|
1
|
1
|
(1 * 2의2승) + (1 * 2의1승) + (1 * 2의0승) = 7(10진수) = 7(8진수)
따라서 2진수 3자리는 8진수 한자리에 해당되므로
아래와 같은 2진수를 8진수로 변환 할때는 3자리씩 끊어서 8진수 한자리로 변환하면 됩니다.
100101= 100 101 = 45 가 됩니다.
또한 3자리로 끊었을때 자리수가 부족하면 0으로 채워서 계산하면 됩니다.
10101 = 010 101 = 25 가 됩니다.
그리고 소수점을 포함한 2진수도 마찬가지 개념으로 변환하면 됩니다.
100101.1011 = 100 101 . 101 100 = 45.54 가 됩니다.
==================================================================
2진수를 8진수,16진수를 변환하는 방법에 대해 위에서 살펴 봤습니다.
그러면 그 역은, 8,16진수를 2진수로 변환하는 방법은 그저 먹기지요??
위 개념을 역으로 하면 될테지요..
별도의 설명이 필요 없겠으나 하나씩만 해 봅니다.
1. 16진수를 2진수로 변환하기
위에서 사용한 수를 가지고 해 봅니다.
위에서 2진수를 16진수로 변환할때 아래와 같았습니다.
11011111 = 1101 1111 = DF
16 진수 DF를 2진수로 변환할려면 16진수 한자리는 2진수 4자리에 해당되므로
D F = 13 15 = 1101 1111 가 됩니다.
소수점을 가지는 16진수도 완전히 동일하겠지요.. 예는 생략 합니다.
2. 8진수를 2진수로 변환하기
역시 위에서 사용한 수를 가지고 해 봅니다.
위에서 2진수를 8진수로 변환할때 아래와 같았습니다.
100101= 100 101 = 45
8진수 45를 2진수로 변환할려면 8진수 한자리는 2진수 3자리에 해당되므로
4 5 = 100 101 가 됩니다.
'SW개발' 카테고리의 다른 글
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
|---|---|
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
| n 진수? 진수 변환 ! (0) | 2023.09.27 |
| 개인정보의 암호화 대상 및 방법 (1) | 2020.07.28 |
| The Scale Cube (규모 확장성 모델) (2) | 2019.02.21 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=95
---
우리가 작성하는 프로그램 코드가 실제 컴퓨터가 어떻게 인식하고 처리 하는지 아는 것은 지극히 기본이며 또한 아주 중요합니다. 실제로 우리가 작성하는 영어에 가까운 언어 문법의 코드 들은 (어떤 언어이든 간에) 컴퓨터는(정확히 말해 CPU는) 단 두가지 수로만 받아 들입니다.
바로 0 과 1 이지요..
인간 언어에 가까운(이를 고급언어라 합니다) C#이나 자바와 같은 언어들은 결국에는 0과 1 로 처리 됩니다. CPU가 처리 할 수 있도록 기계어로 변환 하는 과정은 각 언어의 컴파일러 가 담당하게 됩니다.아래에 컴퓨터 프로그래밍의 기본이 되는 2진수와 기타 진수,진수변환 등을 소개합니다.
* 컴퓨터가 데이터를 인식하는 방법
컴퓨터는 모든 데이터의 연산과 제어를 CPU라는 장치에서 수행합니다
이 CPU는 IC(Integrated Circuit, 집적회로) 의 한 종류입니다

IC 의 모든 핀은 직류 전압 0V 나 +5V 중 하나의 전압을 가집니다.즉, 핀 1개로는 두 가지 상태만 나타낼 수 있습니다.
핀에 전기가 흐를 때는 1 , 흐르지 않을 때는 0을 나타냅니다. 이러한 IC 특성은 컴퓨터의 모든 데이터를 0 과 1 , 즉 2 진수로 처리하게끔 만든 원인입니다.이렇듯 컴퓨터 내부의 트랜지스터가 on / off 상태인 2진수 상태만 기억하므로
컴퓨터는 이 값의 조합으로 모든 데이터를 표현, 처리 합니다
* N 진수
N 진수란 N 개의 숫자를 이용해서 모든 데이터를 표현한다라는 뜻입니다. (16진수의 경우 일부 문자도 포함)
앞서 컴퓨터는 모든 데이터의 표현 및 연산을 0 과 1로 처리한다는 것을 알았습니다. 즉, 0 과 1 두 숫자를 이용해서
데이터를 표현하기에 2진수라 합니다. 우리가 실생활에서 사용하는 10진수는 0 ~ 9 , 10 개의 숫자를 이용해서 모든 숫자를 표현합니다
1.10 진수
10 진수는 0 ~ 9 , 10 개의 숫자를 이용하여 데이터를 표현하는 방식입니다.
데이터 표현>>
0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9
10,11,12,13,14,15,16,17,18,19
……………………………
0 ~ 9 까지 점점 증가하다 9 다음은 다시 0 부터 시작합니다. 즉 9 다음에 자릿수가 증가합니다
2. 2 진수
2 진수는 0 과 1을 이용하여 데이터를 표현하는 방식입니다.
데이터 표현>>
0 , 1
10, 11
100,101,110,111
………………
2진수의 경우 한 자릿수 내에서 표현할 수 있는 최대 값이 1이므로 1 다음에 자릿수가 증가합니다
3. 16 진수
16 진수는 16개의 숫자로 데이터를 표현하는 방식입니다.
단, 숫자는 0 ~ 9 까지만 존재하므로 나머지 6개는 a ~ f 를 사용합니다
데이터 표현>>
0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f
10,11
……………………………..
16 진수의 경우 한 자릿수로 표현할 수 있는 수의 범위가 0 ~ f 이므로 f 다음에 자릿수가 증가합니다
4. 8 진수
8 진수는 8개의 숫자로 데이터를 표현하는 방식입니다
데이터 표현>>
0,1,2,3,4,5,6,7
10,11,12,13,14,15,16,17
8 진수의 경우 한 자릿수 내에서 표현할 수 있는 수의 범위가 0 ~ 7 이므로 7 다음에 자릿수가 증가 합니다.
* 진수 변환
컴퓨터는 2 진수만을 다루지만 사람들은 사용하기 편한 10 진수를 사용합니다. 10진수의 사용기원은 사람의 손가락이 10 개인대서 기원한다고 합니다. 사람들과의 의사소통에는 10진수 표현법으로 의사전달이 가능하지만 컴퓨터는 2진수만 취급합니다. 따라서 프로그래머들은 컴퓨터가 이해하는 2진수로의 변환을 알아야 합니다
10 진수<-> 2진수 나아가 N진수 <-> M 진수로의 변환에 대해 알아보겠습니다
1. 10 진수 <-> 2 진수
먼저 10진수를 2진수로 변환하는 방법을 알아봅니다. 10진수 7을 2진수로 변환합니다.

결과적으로 10 진수 7 은 2 진수 1 1 1 이 됩니다
이제 2 진수를 10 진수로 변경해 보겠습니다. 위의 2 진수 1 1 1 을 10 진수로 변경해 보겠습니다.
계산 방식은 각 자릿수를 2의 승으로 취합니다.
1 1 1 -> (1 * 2의2승) + (1 * 2의1승) + (1 * 2의0승) = 4 + 2 + 1 = 7
2. 10 진수 <-> 16 진수
우선 10 진수를 16 진수로 변경해 보겠습니다. 10 진수 97 을 가지고 변환해 보겠습니다. 계산 방식은 위의 2진수 변경과 동일합니다.

따라서 10 진수 97 은 16진수 61 이 됩니다.
이제 16 진수 61을 10 진수로 변경해 보겠습니다.
61 -> (6 * 16의1승) + (1 * 16의0승) = 96 + 1 = 97
3. 10 진수 <-> 8 진수
우선 10 진수를 8 진수로 변경해 보겠습니다. 10 진수 77 을 가지고 변환해 보겠습니다.

따라서 10 진수 77 은 8 진수 115 가 됩니다.이제 8 진수 115 를 10 진수로 변경해 보겠습니다
115 -> (1 * 8의2승) + (1 * 8의1승) + (5 * 8의0승) = 64 + 8 + 5 = 77
'SW개발' 카테고리의 다른 글
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
|---|---|
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
| 개인정보의 암호화 대상 및 방법 (1) | 2020.07.28 |
| The Scale Cube (규모 확장성 모델) (2) | 2019.02.21 |
| 해킹 피해에 따른 행정처분 사례 (0) | 2019.02.08 |
요즘 블로그가 많이 뜸했군.
다시 블로그 끄적질(?) 시작해야 겠군...
블로그에 글도 없으니, 지난 세월 남는것도 없는 기분!

'일상' 카테고리의 다른 글
| 금연 꿀팁(흡연의 욕구를 단박에 떨쳐버리기) (0) | 2023.10.26 |
|---|---|
| 프로덕트 리더가 반드시 피해야 할 5가지 실수 (0) | 2023.10.10 |
| 성공한 후... (2) | 2022.07.13 |
| 기술사 면접 질문(2016년 4월 그때...) (2) | 2022.02.21 |
| 내가 취득한 자격증과 인증 (2) | 2020.06.03 |
한 미국인 사업가가 의사의 지시에 따라 멕시코의 작은 해안 마을에서 휴가를 보내고 있었다.
첫날 아침, 그는 사무실에서 온 긴급한 전화를 받은 뒤 잠을 이룰 수 없어 머리를 식히려고 부둣가로 나갔다.
부두에는 달랑 어부 한 명이 탄 작은 배가 대어져 있었는데, 그 배 안에는 큼지막한 황다랑어 몇 마리가 있었다.
미국인은 그 멕시코 어부에게 물고기가 아주 훌륭하다고 칭찬을 했다.
“이것들을 잡는 데 얼마나 걸리셨나요?” 미국인이 물었다.
“얼마 안 걸렸수다.” 멕시코인은 놀라울 정도로 완벽한 영어를 구사하였다.
“바다에 더 오래 있으면서 고기를 좀 더 많이 잡지 그러셨어요?” 다시 미국인이 물었다.
“가족을 먹여 살리고 친구들에게도 몇 마리 나눠 줄 만큼 잡았는걸.” 멕시코인은 물고기들을 바구니에 담으면서 말했다.
“하지만…, 남는 시간에는 뭘 하시는데요?”
멕시코인은 미국인을 올려다보더니 미소를 지었다.
“늦잠 자고, 물고기 좀 잡고, 아이들과 놀아 주고, 아내 줄리아와 낮잠을 잔다우. 그러고는 저녁마다 마을을 어슬렁거리다 포도주도 마시고 친구들과 기타를 치면서 놀지. 살고 싶은 대로 살면서 내 딴에는 바쁜 몸이라우.”
미국인은 웃더니 일어났다.
“저는 하버드 MBA 출신으로 아저씨를 도와드릴 수 있습니다. 아저씨는 물고기 잡는 데 더 많은 시간을 투자하고, 그 수익금으로 더 큰 배를 살 수 있습니다. 그러면 머지않아 어획량이 늘어나 배를 몇 척 더 살 수 있을 거고, 나중에는 고기잡이 선단을 갖게 될 거구요.”
그는 계속했다.
“잡은 고기를 중간 상인한테 파는 대신 소비자에게 직접 팔다가 나중에는 통조림 공장을 여는 거죠. 결국에는 아저씨가 제품과 가공, 유통까지 손에 넣게 되는 겁니다. 물론 이 작은 어촌 마을을 떠나 멕시코시티로 옮겨야 할 거고, 그 후에는 로스앤젤레스 그리고 뉴욕까지 진출하는 겁니다. 뉴욕에서는 유능한 경영진과 호흡 맞춰 계속 사업을 확장하며 운영할 수 있을 겁니다.”
“그 모든 일을 이루는 데 얼마나 걸리겠수?” 멕시코인 어부가 물었다.
이 말에 미국인이 대답했다.
“15년에서 20년 정도요. 길어야 25년이죠.”
“그다음엔 어떻게 되우?”
미국인은 웃으면서 말했다. “그게 가장 중요한 부분이죠. 때가 되면 주식을 상장한 후 회사 주식을 팔아서 엄청난 부자가 되는 겁니다. 아마 수백만 달러는 벌게 될 거예요.”
“수백만 달러? 그러고 나서는?”
“그다음엔 은퇴한 후 작은 어촌 마을로 가서 늦잠 자고, 물고기 좀 잡고, 아이들과 놀아 주고, 아내와 낮잠 자고, 저녁에는 어슬렁어슬렁 마을이나 돌아다니며 포도주도 마시고 친구들하고 기타 치며 노는 거죠….”
- 나는 4시간만 일한다(팀 페리스)
과연.. 무엇을 위해 치열해야 하는가...
'일상' 카테고리의 다른 글
| 프로덕트 리더가 반드시 피해야 할 5가지 실수 (0) | 2023.10.10 |
|---|---|
| 다시 블로그 (2) | 2023.09.27 |
| 기술사 면접 질문(2016년 4월 그때...) (2) | 2022.02.21 |
| 내가 취득한 자격증과 인증 (2) | 2020.06.03 |
| 감사하며 살기 (0) | 2020.05.12 |
예전 자료를 보다 우연히 기술사 면접 질문을 정리한 글을 발견했다.
2016년 4월 28일...
108회 정보관리기술사 면접이었으며, 면접 이후 기억에 의존해서 정리한 글이다.
당시 면접 대기실에는 정보분야 뿐만 아니라 다양한 공학분야 기술사들이 같이 면접 대기를 하고 있었다.
나이 지긋해 보이는 분들이 꽤 있었던 것으로 기억한다.
면접관은 총 3분이었으며, 대학교수님과 선배 기술사로 구성되었다고 알고 있다.
편의상 3분을 차례대로 왼쪽분, 중간분, 오른쪽분으로 구분하였다.
아래와 같은 질문들이었는데, 당시 면접 이후 기억에 의존해서 작성되었던 거라 몇 가지 놓친것도 있으리라.
처음 시작...
(중간분) 먼저 편하게.. 여기까지 온 소감을 말해 보세요
본격 질문시작...
(왼쪽분)
- 빅데이터 분석에서 선형성과 등가성에 대한 설명
- 기계학습에서 강화학습과 세미 슈퍼바이저의 차이점
- 포케스트와 프리딕트의 차이점
- 스마트 팩토리를 IoT, 빅데이터 연계해서 설명해 보라
- 하둡 2.0이 나온 배경, 1.0의 어떤 부분이 문제였나?
(중간분)
- 위험과 이슈
- DDoS를 xxx, xxx 관점으로 설명
- VR에서 3D표현을 위해 중요한 기술
- 게임이 산업으로 인정 받으려 한다. 견해는?
(오른쪽분)
- UX설명과 UX설계시 페르소나.. 과정 설명
- 게임피케이션 설명과 사례
- 게임시나리오 어떤 과정으로 작성하나?
- 오픈소스 많이 적용할텐데, 가장 고려해야 할 사항은?
- 프레임워크와 플랫폼의 차이
면접 질문으로 비추어 보아, 왼쪽분은 확실히 빅데이터 전공하시는 교수님 같았다. 학자 스타일이 물씬 풍기는...
그리고 내 경력이 대체로 게임분야이다 보니, 게임 관련된 기술이나 이슈, 트랜드에 대한 질문이 많았던 것 같다.
당시 면접관이셨던 3분께..
좋은 점수 주셔서 이자리를 빌어 감사 드립니다 ^.^
요즘 개인정보가 핫(hot)? 하다.
산업 전 분야에 걸쳐 개인정보가 주요한 비즈니스 데이터로 활용되고 4차 산업혁명의 인공지능, 빅데이터, 사물인터넷 등의 융/복합 기술 기반에는 방대하고 광범위한 데이터가 활용되는데 여기서 개인정보 역시 예외가 아니다.
하지만 무분별한 개인정보의 활용은 많은 부작용을 낳는 것도 사실이다.
기업이나 개인은 타인의 개인정보를 활용할 때, 자칫 잘 못 하면 법 방망이(?)에 후드려 맞을 수 있다는 것을 명심해야 한다.
보통 개인정보를 정보시스템에 저장 또는 송/수신할 때 암호화 해야 한다고 알고 있는데, 그 기준이 모호할 때가 많다.
"모든 개인정보를 암호화 해야 하는가? 개인정보의 범위는 어디까지 인가?"
이 글에서는, 법령과 행정규칙에 근거하여 개인정보의 개념을 이해하고 암호화 대상과 방법에 대해 알아보고자 한다.
By 개인정보보호법
'개인정보보호법'에서는 '개인정보'를 다음과 같이 정의하고 있다.
[개인정보보호법, 제2조(정의)]
"개인정보"란 살아 있는 개인에 관한 정보로서 다음 각 목의 어느 하나에 해당하는 정보를 말한다
- 성명, 주민등록번호 및 영상 등을 통하여 개인을 알아볼 수 있는 정보
- 해당 정보만으로는 특정 개인을 알아볼 수 없더라도 다른 정보와 쉽게 결합하여 알아볼 수 있는 정보. 이 경우 쉽게 결합할 수 있는지 여부는 다른 정보의 입수 가능성 등 개인을 알아보는 데 소요되는 시간, 비용, 기술 등을 합리적으로 고려해야 한다.
- 가명처리함으로써 원래의 상태로 복원하기 위한 추가 정보의 사용,결합 없이는 특정 개인을 알아볼 수 없는 정보(가명정보)
(참고) 가명처리
- 개인정보의 일부를 삭제하거나 일부 또는 전부를 대체하는 등의 방법으로 추가 정봅가 없이는 특정 개인을 알아볼 수 없도록 처리하는 것
법령 정의에 근거하여 개인정보를 해석하더라도, 개인정보의 범위는 매우 광범위 할 수 있으며 상황에 따라 해석이 달라질 수 있는 것을 알 수 있다
개인정보보호법의 '개인정보의 안전성 확보조치 기준'에서는 개인정보 암호화 대상 및 방법을 명시하고 있다.
[개인정보의 안정성 확보조치 기준, 제7조(개인정보의 암호화)]
- 고유식별정보/비밀번호/바이오정보를 정보통신망으로 송신하거나 보조저장매체 등을 통하여 전달하는 경우
- 비밀번호/바이오정보를 저장하는 경우(단 비밀번호를 저장하는 경우 복호화 되지 않도록 일방향 암호화 저장)
- 인터넷 구간 및 DMZ에 고유식별정보를 저장하는 경우
- 내부망에 고유식별정보를 저장하는 경우 다음 각 호의 기준에 따라 암호화 적용여부/범위 정하여 시행
- 개인정보 영향평가의 대상이 되는 공공기관의 경우 해당 개인정보 영향평가 결과
- 암호화 미적용시 위험도 분석에 따른 결과
- 개인정보를 암호화 하는 경우 안전한 암호알고리즘으로 암호화 저장
- 암호화된 개인정보를 안전하게 보관하기 위해 안전한 암호 키 생성, 이용, 보관, 배포 및 파기 등에 관한 절차 수립/시행
- 업무용 컴퓨터 또는 모바일 기기에 고유식별정보를 저장하여 관리하는 경우 상용 암호화 SW 또는 안전한 암호화 알고리즘을 사용
(고유식별정보)
- 주민등록번호 / 외국인등록번호 / 운전면허번호 / 여권번호
(암호화 미적용시 위험도 분석에 따른 결과)
- 개인정보처리시스템의 보호수준을 진단하여 암호화에 상응하는 조치를 했는지를 분석
- (참고) 개인정보 위험도 분석 기준 및 해설서
글로 나열된 법 조문으로는 한눈에 들어오지 않는다. KISA(한국인터넷진흥원)에서 발간한 '개인정보의 암호화 조치 안내서'의 요약표를 옮겨 보았다.

또한 해당 안내서에서는 안전한 암호 알고리즘을 안내하고 있다.
- 안전한 암호 알고리즘이란 국내 및 미국, 일본, 유럽 등의 국외 암호 연구 관련 기관에서 권고하는 암호 알고리즘을 의미
- 공공기관은 국가정보원의 검증대상 암호 알고리즘을 기반으로, 민간부문(법인,단체,개인)은 국내/외 전문기관(KISA, NIST, ECRYPT, CRYPTREC 등)이 권고하는 암호 알고리즘을 기반으로 개인정보보호법상의 개인정보 암호화에 사용할 수 있는 안전한 암호 알고리즘의 예시는 다음의 표와 같다.

By 정보통신망법
개인정보보호법 뿐만 아니라, 정보통신망법에서도 '개인정보의 기술적/관리적 보호조치 기준'을 통해 개인정보 암호화에 대한 행정 규칙을 명시하고 있다.
[개인정보의 기술적/관리적 보호조치 기준, 제6조(개인정보의 암호화)]
- 비빌번호는 복호화 되지 않도록 일방향 암호화해서 저장
- 다음 각 호의 정보를 안전한 암호알고리즘으로 암호화해서 저장
- 주민등록번호
- 여권번호
- 운전면허번호
- 외국인등록번호
- 신용카드번호
- 계좌번호
- 바이오정보
- 개인정보 및 인증정보를 송/수신할 때에는 안전한 보안서버 구축 등의 조치. 보안서버는 다음 각 중 하나의 기능을 갖추어야 함
- 웹서버에 SSL 인증서를 설치하여 전송 정보 암호화 송/수신 기능
- 웹서버에 암호화 응용프로그램을 설치하여 전송 정보 암호화 송/수신 기능
- 개인정보를 컴퓨터, 모바일 기기 및 보조저장매체 등에 저장할 때에는 암호화
개인정보보호법과 거의 유사하지만, 암호화 대상에 있어 두 가지(신용카드번호, 계좌번호)가 추가되어 있는 것을 확인할 수 있다.
결론
지금까지 관련 법령(개보법/정통망법)과 행정규칙을 살펴 보았는데, 쉽게 풀어서 결론 지으면 다음과 같다.
1. 고유식별정보(주민등록번호/운전면허번호/여권번호/외국인등록번호)와 비밀번호, 바이오정보는 무조건 암호화
(내부망 저장시 예외가 있긴 하나, 이는 한정된 기관(일부 공공기관 등)에 한하므로 패스. 상세한 내용은 위의 표 참조)
2. 암호화 할 때는 안전한 암호화 알고리즘을 사용
(안전한 알고리즘은 위에 표 참조)
3. 비밀번호는 (복회화 되지 않도록) 일방향 (해쉬) 암호화
4. 정통망법 적용 사업자는 추가로 신용카드번호, 계좌번호도 암호화
(주의)
이 글에서는 두개의 법(개보법/정통망법)만을 참조하여 작성되었습니다.
분야별로 법 적용이 다를 수 있으므로 사업자별로 적용받는 법(신용정보법, 위치정보법 등)을 추가로 확인해야 할 수도 있습니다.
(참고) FAQ
KISA가 발간한 '개인정보 암호화 조치 안내서'에는 실무자들이 암호화 조치 관련하여 자주 궁금해 하는 점들을 부록의 FAQ로 안내하고 있는데, 여기에 그 내용을 옮겨와 본다.
[Q1] . 개인정보 보호법 상의 암호화 대상은 무엇이며 어떻게 암호화해야 하나요?
개인정보 보호법상 암호화 대상은 고유식별정보(주민등록번호, 외국인등록번호, 운전면허번호, 여권번호), 비밀번호, 바이오정보입니다. 암호화 대상 정보를 전송시 그리고 저장시 아래 표에 따라 암호화하여야 합니다

[Q2]. 공공기관입니다. 개인정보처리시스템의 DBMS (DataBase Management System)에서 제공하는 TDE(Transparent Data Encryption) 방식을 사용한 암호화가 개인정보 보호법에 위배됩니까?
개인정보 보호법 관점에서는 개인정보의 안전성 확보조치 기준(고시)에 따라 고유식별정보 암호화시 안전한 알고리즘을 사용하도록 하고 있습니다. TDE 방식에서 안전한 알고리즘을 사용하여 암호화한다면 법 위반 사항이 아닙니다. 다만, 공공기관은 전자정부법에 따라 국가정보원이 안전성을 확인한 암호모듈 또는 제품을 우선 적용하여야 하며 자세한 사항은 해당 기관에 적용되는 관련 법령, 고시, 규정, 지침 등을 확인하시기 바랍니다
[Q3]. 암호화 관련하여 우리 기관(공공, 민간)에 적용되는 규정·지침과 개인정보보호법에서 적용하는 암호화 요구사항이 서로 다를 때 어느 것을 적용해야 하나요?
개인정보 보호법 및 시행령, 고시에서 규정한 암호화 요구사항을 준수하면 개인정보 보호법상 암호화 의무는 준수한 것입니다. 본 고시 준수로 인하여 다른 규정·지침을 준수하기 어렵게 된다면 “개인정보 보호법”은 준수 하였으나 해당 규정·지침은 위배한 것이 될 수 있습니다. 따라서, 최선의 방법은 개인정보 보호법과 해당 기관에 적용되는 규정·지침에서 요구하는 암호화 관련 사항 모두를 준수하는 것이라 할 수 있습니다.
[Q4]. 안전한 암호 알고리즘에는 어떤 것들이 있나요?
안전한 암호 알고리즘은 국내·외 전문기관에서 권고하고 있는 알고리즘으로서 본 안내서의 ‘[참고 1] 국내·외 암호 연구 관련 기관의 권고 암호 알고리즘’, ‘[참고 2] 국가정보원 검증대상 암호 알고리즘 목록’의 내용을 참고하시기 바랍니다
[Q5]. 대칭키 암호 알고리즘 DES나 해쉬함수 MD5를 사용하면 안 됩니까?
DES와 MD5와 같은 암호 알고리즘의 경우 안전성 유지가 어려우므로 안전한 암호 알고리즘으로 볼 수 없어 권고하고 있지 않습니다. 안전한 암호 알고리즘은 본 안내서의 ‘[참고 1] 국내·외 암호 연구 관련 기관의 권고 암호 알고리즘’, ‘[참고 2] 국가정보원 검증대상 암호 알고리즘 목록’ 내용을 참고하시기 바랍니다.
[Q6]. DB에 저장된 주민등록번호를 일부분만 암호화해서 저장해도 되는 것인지요?
예, 일부분 암호화가 가능합니다. 시스템 운영이나 개인 식별을 위해 해당 정보를 활용해야 하는 경우 생년월일 및 성별을 포함한 앞 7자리를 제외하고 뒷자리 6개 번호를 암호화 하여 사용할 수도 있습니다.
[Q7]. 암호화해야 하는 바이오정보의 대상은 어디까지 인지요?
암호화하여야 하는 바이오정보는 식별 및 인증 등의 업무절차상 수집이 명확한 경우로 한정되며, 이와 무관하게 수집되는 이미지, 녹취 정보 등은 암호화 대상에서 제외됩니다. 예를 들어, 콜센터 등에서 업무절차상 주민등록번호 수집이 명확한 경우의 음성기록은 암호화 해야 하나, 단순 상담 시 저장되는 음성기록 등은 암호화 대상에서 제외될 수 있습니다.
[Q8]. 안전한 대칭키 암호화 알고리즘 사용시 암호키(비밀키)의 길이는 어떻게 설정해야 하나요?
암호키의 길이가 짧거나 사용되는 문자의 종류를 섞어 쓰지 않으면 암호화가 되었더라도 공격자가 쉽게 암호 해독을 할 수 있습니다. 암호해독이 어렵도록 암호키 설정시 문자, 숫자, 특수문자 등의 문자조합 방법과 문자열 길이, 사용기간 등의 암호키 작성 규칙을 정하여 운영하는 것이 바람직합니다. 특히 잘 알려진 영문자, 숫자(1234, 123456, love, happy, admin, admin1234) 등은 쉽게 유추 할 수 있으므로 사용하지 않도록 주의해야 합니다.
[Q9]. 회사에 고객들의 이름, 주소, 전화번호, 이메일, 비밀번호를 저장하고 있습니다. 암호화 대상이 무엇인가요?
개인정보의 안전성 확보조치 기준 고시에서 암호화 대상은 고유식별정보(주민등록번호, 여권번호, 운전면허 번호, 외국인등록번호), 비밀번호, 바이오정보입니다. 특히, 비밀번호의 경우에는 일방향(해쉬) 암호화하여 저장하시면 됩니다
[Q10]. 부동산중개업을 하고 있습니다. 업무용 컴퓨터에 한글, 엑셀을 이용하여 주민등록번호를 처리 하고 있습니다. 암호화를 어떻게 해야 합니까?
PC에 저장된 개인정보의 경우 상용프로그램(한글, 엑셀 등)에서 제공하는 비밀번호 설정기능을 사용하여 암호화를 적용하거나, 안전한 암호화 알고리즘을 이용하는 소프트웨어를 사용하여 암호화할 수 있습니다.
※ 한컴 오피스 : 파일 >> 다른이름으로 저장하기 >> 문서 암호 설정에서 암호 설정 가능 ※ MS 오피스 : 파일 >> 다른이름으로 저장하기 >> 도구 >> 일반옵션에서 암호 설정 가능
[Q11]. A사가 개인정보처리시스템을 위탁하거나, ASP(Application Service Provider), 클라우드 서비스를 이용하는 경우 암호화 수행을 누가 해야 하나요?
개인정보의 암호화 등 안전성 확보조치는 원칙적으로 “개인정보처리자”의 의무입니다. 따라서 개인정보 처리시스템을 위탁하거나 ASP를 이용하는 경우에도 암호화 조치사항에 대한 이행여부에 대한 책임은 위탁기관인 A사가 지게 됩니다. 다만, A사는 암호화에 대한 요구사항을 A사의 위탁을 받은 수탁기관(ASP, 클라우드 서비스 제공자 등)과의 계약서 등에 명시하여 수탁기관으로 하여금 암호화를 처리하게 요구할 수 있습니다.
'SW개발' 카테고리의 다른 글
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
|---|---|
| n 진수? 진수 변환 ! (0) | 2023.09.27 |
| The Scale Cube (규모 확장성 모델) (2) | 2019.02.21 |
| 해킹 피해에 따른 행정처분 사례 (0) | 2019.02.08 |
| [웹보안] SQL Injection (1) | 2019.01.28 |
나에게 자격증은 일종의 도전이자 동기부여의 한 수단 이었다.
그리고 내 직무/전문분야에 대한 정리이자 증명의 수단이기도 했다.
그래서 나는 (운전면허를 제외하고는) IT 분야 자격증만 취득해 왔다.
그간 취득한 자격증과 인증을 (취득 날짜 순으로) 정리해 보기로 한다.
인터넷 정보검색사 2급
(발행기관) 한국정보통신진흥협회
(취득일) 2001년 ?월 (몇 월 이었는지 기억도 안남)
군대를 제대하고 복학을 하니, 인터넷이란 것이 유행(?) 했더랬다. 당시 수업도 인터넷과 관련된 새로운 과목도 개강을 하여 들었던 기억이 난다.
사실 이 자격증은, (바로 아래에 있는) 전자상거래관리자 자격증을 준비하면서 재미로(?) 시험을 본 자격증이다.
(꽤 넓은 범위를 다루고 있는) 전자상거래관리사 자격증 공부 영역 중 일부에 해당하기도 했었고, 시험 자체가 집에서 컴퓨터로 온라인 시험을 보고, 결과도 그 자리에서 바로 나와서 아주 쉽게 취득한 자격증이다. 물론 그만큼 가치도 별로 없다.
이 자격증은 내 이력서에서도 제외하곤 하지만, 그래도 내 첫 IT 분야 자격증이니 여기에 기록해 본다.
전자상거래관리자 2급
(발행기관) 대한상공회의소
(취득일) 2001년 7월
대학 졸업반 시절, IT 관련 일을 준비하면서 취득하게 된 자격증이다.
당시 이 자격증의 광고와 홍보가 많이 이루어졌고, 뭔가 그럴싸해 보였다.(돌이켜 보니 광고에 혹했고 내가 순진했다.)
당시 정보처리기사급 정도 되었던 것 같다. (당시 지인이 옆에서 정보처리기사를 공부했더랬다)
1차 필기/2차 실기 시험 이었는데, 1차 필기는 다루는 범위가 꽤나 방대했었고
2차 필기는 직접 컴퓨터를 가지고 각종 작업(IIS 웹서버 셋팅/ASP 등)을 해야 해서 나름 공부 많이 하고 취득한 자격증이다.
OCP(Oracle Certified Professional) 9i
(발행기관) Oracle
(취득일) 2004년 3월
오라클이라는 외국의 유명한 DBMS 회사에서 주최하는 자격 시험이다.
실무에서 DB를 다루기도 하고, 뭔가 있어 보이기도 하고, 학원에 자격반 커리큘럼도 있고 해서 준비하게 되었다.
필기 시험으로만 취득하는 페이퍼 자격증이라는 오명을 벗기 위해, 9i 버전 부터는 일정 시간 이상 실무 교육을 필수로 요구했었다.
그래서 꽤 비싼 수강료를 지불하고 실무 강의도 수강했었다. 매일 저녁 멀리 있는 학원에 가는게 매우 귀찮았던 걸로 기억한다.
MCAD (Microsoft Certified Application Developer)
(발행기관) Microsoft
(취득일) 2005년 1월
부산의 동명정보기술원이라는 기관에서 같이 공부하던 여러 사람들과 같이 준비하고 취득한 자격증이다.
마이크로소프트에서 주최하는 국제 자격증으로 MS 기반 개발자를 위한 자격 인증 시험이다.
당시에는 MCAD, MCSD, MCT 로 이어지는 도전을 생각했으나, 이 자격증 까지만으로 만족(?)해 버렸다.
MS MVP(Microsoft Most Valuable Professional), C# 부문
(발행기관) Microsoft
(취득일) 2008년 7월
이건 자격증이 아니라 인증 프로그램이다. 마이크로소프트에서 자사의 각 기술 분야에 대한 전문가를 인증하는 프로그램으로 별도의 자격 시험을 치루는 게 아니라, 전문가 활동을 한 내역 증명과 심사 통과가 필요하다.
전문가 활동이란, 해당 기술 분야에 대한 책을 쓰기나 강의를 하거나 기술 블로그 등에 글을 작성 하거나 Q&A에 답변을 하는 등 그 활동으로 인해 '해당 기술을 널리(?) 알리고 타인을 (기술적으로) 도와 주었는가?'를 심사한다.
자신의 전문가 활동 내역을 정리해서 영문으로 (제공되는) 포맷에 맞게 제출하면 심사가 이뤄지는데,
'한국 -> 아시아 -> MS 본사' 순으로 심사가 진행되는 것으로 기억한다.
MS 제품과 관련한 다양한 분야의 MVP를 선발하는데, 나는 당시 실무에 주력 언어로 사용하던 C# 부분에 지원 했었다
처음 시도 했을 때, 한번 미끄러지고 두 번째 시도에 통과했었다.
당시 MS MVP는 공신력도 있었고, MS 계열 엔지니어들에게서 꽤 선망의 대상이어서 심사에 통과하고 많이 뿌듯했었다.
PMP(Project Management Professional)
(발행기관) PMI
(취득일) 2009년 6월
2008년부터 팀장 직무를 수행하게 되었는데, 이 때 프로젝트 관리에 관심을 가지게 되었고 이왕 하는거 제대로 해 보자는 마음으로 준비하게 된 자격증이다.
국제적 프로젝트 관리 기관인 PMI(Project Management Institute)에서 프로젝트 관리 전문가에게 부여하는 자격증이다.
이 자격증을 위해 라이지움이라는 학원도 다녔었다. 공부할 내용이 방대하고 복잡한 계산 문제도 있어서 정성을 꽤나 쏟았다.
시험 보는 날이 아직 머리속에 생생하다. 시험은 정해진 시험 장소에 가서 컴퓨터로 치룬다. 시험 결과는 시험 종료 후 최종 제출을 하면 몇 분 기다리다가 바로 나온다. 그 몇 분의 떨림이란...
첫번 째로 응시한 시험에 (운 좋게) 합격하여, 기분 좋게 복귀 했던게 생각난다.
기술사(정보관리)
(발행기관) 한국산업인력공단
(취득일) 2016년 5월
이건 매우 비장한 각오로 준비한 자격증이다. 혹독한 준비 과정을 각오했으며 주말도 반납하며 공부 했었다.
1차 논술 시험과 2차 면접 시험으로 구성되어 있다.
1차 시험은 1교시 90분씩 총 4교시 시험을 치르게 되는데, 시험 시간만 자그마치 6시간이다.
이 6시간을 혼신의 힘을 다해 논술해 나가야 한다. 오전 9시에 시작해 오후 6시 조금 전에 시험을 마치는데 시험을 치고 나면 녹초가 되는 기분이었다.
2차 시험은 대학교수/기술사로 구성된 3명의 면접관 앞에서 (외로이?) 질문에 성실히 답해야 한다. 기술적인 답변을 잘 하는 것이 제일 중요하나, 구술시험이다 보니 임기응변과 순발력과 재치도 필요하다.
이 자격증은 1차 시험 합격이 중요한 시험이다. 2차에 비해 1차의 합격률이 매우 낮으며 2차 시험은 1차 합격 이후 4번 정도의 기회가 부여 되기 때문에, 1차 합격하면 기술사가 된 것으로 인정하는 분위기이다. (물론 2차에 고배를 여러차례 마신 분들도 있긴 하다)
나의 경우, 1차 시험 합격 기준으로 총 1년 6개월 정도 걸렸으며 (6개월 마다 있는 시험 일정에) 총 3번의 시험을 치뤘다.
첫번째 시험은 공부 시작한지 얼마 안되서, (기대도 없이) 경험삼아 보게 되었고, 두 번째 시험은 작심하고 봤다.
두 번째 시험에서 살짝 아깝게 떨어지고, 세 번째 시험에 (운좋게) 합격하게 되었다. 면접도 한번에 붙어서 매우 기뻤다.
매우 힘든 과정과 시험이었지만, 뭔가를 (오랜 기간) 제대로 준비하고 모든 것을 쏟아 부어 성취한 느낌을 주게 한 소중한 자격증이다.
2017/12/22 - [자격증] - [기술사] 철지난 합격수기
2016/10/09 - [자격증] - KPC 공개설명회
정보시스템 수석감리원
(발행기관) 정보시스템감리협회
(취득일) 2016년 7월
기술사 자격을 취득하면 (별도의 시험이나 감리 경험 없이) 5일간의 감리교육만 이수하면 수석감리원 자격이 부여된다. 기술자 자격의 혜택 중 하나이다.
실제 감리를 수행하는 과정이 교육 커리큘럼이라 5일간 꽤 낯설고 힘들었던 기억이 난다.
교육 마지막날 소정(?)의 필기 시험이 있는데 교육을 충실히 듣고, 공부 조금 했다면 그리 어렵지 않게 통과할 수 있다. 물론 그 전에 기술사 공부로 어느정도 감이 있어서 도움이 되었다.
데이터 품질인증(DQC-V) 심사원
(발행기관) 한국데이터진흥원
(취득일) 2016년 8월
한국데이터진흥원에서 주최하는 데이터 관련 3종 인증 심사원 중 데이터 품질에 관한 심사원 자격이다.
3일간(2일인가? 기억이 가물)의 교육, 주말 시험으로 취득할 수 있다.
교육은 참신하고 재미있었는데... 이 시험이.. 만만하게 볼 게 아니다.
아무래도 실무 현장에 가서 의뢰 기관의 데이터 품질을 객관적으로 측정하는 일을 해야 되다 보니, 시험에 신경을 꽤 쓴 느낌이었다.
중요한 것은, 다른 심사원 자격보다 보수가 짭짤한 것이 장점이다ㅏ.
2016/09/29 - [자격증] - 데이터 품질(DQC-V) 인증심사원
ISMS-P (정보보호 및 개인정보보호 관리체계 인증)
(발행기관) KISA
(취득일) ISMS: 2016년 10월 / ISMS-P: 2019년 5월
기업(기관)의 정보보호관리체계/개인정보보호관리체계를 점검하고 심사하는 인증 심사원을 양성하기 위한 자격 시험이다.
2016년에 필기 시험 치고, 5일간 실무 교육 받고 ISMS 심사원 자격을 취득했다.
이후 ISMS와 PIMS가 ISMS-P로 통합 되면서 이틀간 전환 교육 받고 필기시험 한번 떨어지고,
재시험에 통과하여 최종적으로 ISMS-P 심사원 자격을 취득했다.
필기 시험이 쉽지 않다.
과거에는 교육만 받으면 자격이 나왔다고 하는데, 심사원의 전문성과 자질 문제가 불거지면서 필기 시험이 도입되었다.
그 필기가 도입되고 얼마 안되 2016년에 내가 시험을 보게 된 것이다.
문제 수도 많고, 각 문제 지문도 길고, 다지 선다(압권은 모두 고르시오)에..
2016년 당시 시험 시간이 턱없이 부족했었던 기억이 난다. 정말 꾸역꾸역 시험을 쳤는데 진짜 운 좋게 합격한 것 같다.
2019년에 ISMS-P 시험은 2016년 당시 시험 보다는 여유롭게 봤지만 쉽지는 않았다.
2016/10/29 - [자격증] - ISMS 인증심사원 자격취득
소프트웨어 보안약점 진단원
(발행기관) KISA
(취득일) 2017년 11월
말 그대로 소프트웨어의 보안 약점을 진단하는 심사원 양성을 위한 자격증이다.
5일간의 교육과 마지막날 필기 시험을 치러야 한다.
필기 시험이 꽤 어렵다.
(ISMS-P도 그렇고) KISA는 시험 난해하게 내기로 작정한 모양이다. ㅋ
물론 심사원 취득 과정이 험난(?)해야 제대로 된 심사를 하니깐 난해함을 존중하는 바이다.
이상..
그간 취득한 자격증을 정리해 봤다.
치열했던 나의 도전에 박수를 보낸다 !!!
'일상' 카테고리의 다른 글
| 성공한 후... (2) | 2022.07.13 |
|---|---|
| 기술사 면접 질문(2016년 4월 그때...) (2) | 2022.02.21 |
| 감사하며 살기 (0) | 2020.05.12 |
| 기술사 블로그 (3) | 2018.06.25 |
| 소프트웨어 보안약점 진단원 (6) | 2018.03.01 |
늘 같은 일상이 반복되면서,
나에게 주어진 소중한 것들을 너무나도 당연시 여기며 살고 있다는 것을 ...
심지어 여기에서 진화하여,
사소한 불편에 집중하고 중대한 불만으로 승화(?) 시키고 있다는 것을 ...
일상의 출근길 가운데 불현듯 뇌리를 스쳐 지나갔다.
감사하며 살아야 겠다고 다시 다짐해 본다.
감사하며 살되, 나태해 지지는 말자라고...

'일상' 카테고리의 다른 글
| 기술사 면접 질문(2016년 4월 그때...) (2) | 2022.02.21 |
|---|---|
| 내가 취득한 자격증과 인증 (2) | 2020.06.03 |
| 기술사 블로그 (3) | 2018.06.25 |
| 소프트웨어 보안약점 진단원 (6) | 2018.03.01 |
| 부산과 바다 (0) | 2018.02.20 |
아마... 아래 그림은 한번쯤은 본 적이 있을 겁니다.
개개인의 서로 다른 재능을 무시한채, 획일적인 기준으로 평가하는 문제를 풍자하는 그림인데요..
"공정한 선발을 위해 같은 시험을 봐야 합니다: 모두 저 나무에 올라 가세요" (말풍선)
"모두가 천재다. 그러나 나무에 오르는 능력으로 물고기를 판단한다면, 그 물고기는 평생 자신을 멍청하다고 생각하며 살아갈 것이다" - 아인슈타인
이 카툰은 획일적인 교육과 평가에만 의존하는 교육분야의 문제 인식으로 자주 인용되지만, 기업의 경영 전략에도 대입해 볼 수 있다는 생각이 듭니다.
기업의 존재 목적은 수익 창출입니다. 모든 기업은 수익을 창출하기 위해 다른 기업과는 차별화된 재화나 서비스를 시장에 공급합니다. 이러한 수익 창출 과정에서 주어진 자원을 최대한 효율적으로 사용해서 수익을 극대화 시키고 리스크(risk)를 경감하는 것이 중요합니다.
따라서 기업은 자신이 제공하는 핵심 서비스 전개를 위한 업무 역량은 자체적으로 내재화 시켜서 경쟁력을 확보하고 다른 기업과의 차별화를 꾀해야 합니다.
반면, 핵심 서비스에 직접적이지 않은 비 핵심업무는 다른 기업이나 다른 사람에게 위임하여 그들의 전문성을 활용하는 것이 좋습니다. 그렇게 해야 생산성이 향상하고 리스크를 경감할 수 있습니다.
기업의 외주(아웃소싱) 전략에 좋은 참조 모델이 있어 소개하고자 합니다.
---
'캐즘(Chasm) 이론'으로 유명한 제프리 A.무어의 '코어/컨텍스트(Core/Context) 모델'은 기업이 주어진 자원을 어떻게 운용하는 것이 좋을지에 대한 참조 모델을 제시하며 '클라우드 충격'이라는 책에서 자세히 설명하고 있습니다.
코어(Core)란 의미 그대로 기업의 핵심 업무를 말합니다. 코어 업무는 기업의 경쟁우위를 높여주는 중요한 것이므로 최대한 자원을 집중해야 하고 자체 개발을 해야 한다는 것입니다.
반면 컨텍스트(Context)는 코어 이외의 모든 활동이라고 말합니다. 컨텍스트 업무는 차별성을 추구하는 것이 아니라 가능한 표준적인 방식으로 효율을 최우선으로 수행하는 것'이 좋다고 말합니다.
또한 이러한 컨텍스트 업무는 어느 누군가에게는 코어 업무이기 때문에 그쪽에 아웃소싱을 맡길 수 있다고 시사합니다.
게임을 개발하는 기업에서 인사관리 프로그램이 필요한 사례를 예로 들어 보겠습니다.
게임 개발은 회사의 중요한 코어 업무이기 때문에 자체 개발을 해야 하며, 인사관리 프로그램은 컨텍스트 업무이기에 그 업무를 코어로 하는 외부 업체에게 아웃소싱 하는 식입니다.
그러나 코어/컨텍스트만으로는 기업내 모든 활동을 양분하기에는 한계가 있어 보입니다.
무어는 코어/컨텍스트 구분과 더불어, '미션크리티컬/'비미션크리티컬' 이라는 또 하나의 축을 또 다른 기준으로 내세웠습니다. 미션 크리티컬은 만일 중지되었을 때 즉시 심각한 리스크로 이어지는 기업 활동을 말하며 그 외의 모든 업무는 비 미션크리티컬이 됩니다. 즉 리스크의 정도를 기준으로 삼고 있습니다.
이에 대한 도식은 아래와 같습니다.
[출처: 클라우드의 충격]
---
제가 속해 있는 IT 분야에서도 아웃소싱 전략에 큰 영향을 주는 두가조 요소가 있습니다.
바로 클라우드(Cloud)와 오픈소스(Opensource)입니다.
오픈소스의 경우 외주(아웃소싱)라는 카테고리와는 성격이 조금 다를 수 있지만, 특정한 업무를 외부 자원으로 해결한다는 위임이라는 측면에서는 맥을 같이 하기에 연결지어 봤습니다.
클라우드의 경우 종전의 자체 전산실에 직접 렉과 장비를 구비하고 운영했던 온프레미스(On-Premise) 환경과는 달리 클라우드 환경에서는 이러한 물리적인 장비와 운영체제, 소프트웨어까지 빌려 쓸 수 있게 되었습니다. 또한 기업은 자신들이 어디 까지를 직접 운영할지 결정하여 Iaas, Paas, Saas 형태의 클라우드 서비스 모델을 선택할 수 있습니다.
갈수록 IT 환경의 판이 많이 달라지고 있습니다. 자원을 최적화 시키는 것은 기업의 생산성을 향상시키는 것 뿐만 아니라, 서로 다른 재능을 가진 기업간 위임이 활성화 되어 산업의 발전에도 기여하게 된다고 봅니다. 과거 분업화가 많은 발전을 야기한 것 처럼요.
현재 자신의 회사나 수행하는 프로젝트에서, 코어와 컨텍스트, 미션크리티컬과 비미션크리티컬의 4사분면에 해당하는 업무가 무엇인지 파악하여 전략을 재정비 해 보는 것도 좋을 것입니다.
'프로젝트관리' 카테고리의 다른 글
| [PMP] 시간관리-활동 정의,관계,순서 부여 (2) | 2023.10.24 |
|---|---|
| [PMP] 시간관리 - 프로세스 개요도 (2) | 2023.10.24 |
| Tuckman의 팀 발달 모델 (1) | 2019.03.07 |
| 데브옵스 처방전 (0) | 2015.05.21 |
| 개발자 칠거지악 (0) | 2015.02.06 |




