[컴퓨터의 실수표현]검색결과, 4건
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=530
---
(이 글은 닷넷 프레임워크 기반의 예제 및 개념입니다. 그러나 대부분의 개념은 언어와 무관합니다)
여러분들은 '실수 연산'을 할 일이 있나요?
간혹, 랜덤한 값을 계산하거나, 그래프를 그릴 때, 간혹 실수 연산을 할 일이 있을 겁니다
그러나 이 경우에는 정확한 결과가 나오지 않아도 되는 경우가 많습니다
따라서 질문을 다시 해 보죠
여러분들은 정확한 실수 연산을 할 일이 있나요?
다음의 코드의 실행 결과를 예상해 보세요
double a = 11.22;
double b = 11.10 + 0.12;
bool result = (a == b);
result 는'참' 일까요, '거짓' 일까요?
인간의 계산(?) 방식대로 하면, 11.10 + 0.12 = 11.22 이기 때문에 a, b 두 값은 같으니까, 결과는 '참' 이어야 겠죠
그러나 결과는 '거짓' 입니다
컴퓨터는 인간처럼 계산하지 않는다는 게 원인이죠
이와 관련해서 자세한 내용은, 다음의 제 글들을 확인해 주세요
-> 0.1 을 100 번 더해도 10이 되지 않는다?
-> 실수 데이터의 표현 방식 - 부동소수점 방식
-> +- m * ne
그러면, 위 코드에 의해, 컴퓨터가 계산한 결과를 볼까요?
실수의 부동소수점 표현을 보기 위해 C# 에서 Console.WriteLine 에 형식 문자열(E/e)로 16자리까지 봅시다
double a = 11.22;
double b = 11.10 + 0.12;
Console.WriteLine("{0:e16}", a);
Console.WriteLine("{0:e16}", b);

어떻습니까?
두 값은 엄연히 다릅니다. 이것이 바로 컴퓨터가 계산한 결과 입니다
위에 제시한 링크의 글들을 보셨다면 이유는 아셧을 겁니다
컴퓨터가 실수를 표현하는 부동소수점 방식은 특정한 식에 의해 최대한의 근사치 만을 표현하기 때문입니다
---------------------------------------------------------------------------------------------------
참고로, 우리나라 화폐단위는 (간편하게도) 소수점이 없죠.
미국 화폐의 경우 센트 단위가 있어, 화폐 계산 할 때 소수점 연산이 필요한 경우가 있습니다
돈이 걸린 문제는 민감하죠. 그래서 돈 계산에 실수가 사용된다면 정확한 결과를 보장해야 겠지요
그런데, 문제는 실수 연산은 정확하지 않다는 겁니다
더 정확하게 말하자면, 부동소수점 방식의 실수 연산을 정확하지 않다는 거죠
만일, 돈 계산과 같이, 실수 연산이 매우 정확해야 한다면 부동 소수점을 사용하면 안됩니다
대표적인 부동 소수점 데이터타입으로는 float(single) 과 double 이 있죠
즉 실수를 double 로 선언해서 돈 계산을 하면 안된다는 말입니다
가장 간편한(?) 방법은 decimal 데이터 타입을 사용하는 것이죠
msdn의 다음문구를 참고하세요
'Single 및 Double에서는 정확하지 않는 숫자가 Decimal에서는 정확하게 표시되는 경우가 있습니다(예: 0.2, 0.3).
Decimal에서는 부동 소수점에서보다 산술 연산이 더 느리지만 더 정확한 결과가 나타나므로 성능 감소를 감내할
만한 가치가 있습니다'
그리고 중요한 것은 현재 환경에 맞는 최적의 선택이죠. msdn은 이렇게 권고합니다
'Decimal 데이터 형식은 모든 숫자 형식 중 가장 느린 형식입니다. 데이터 형식을 선택하기 전에 정밀도와 성능 중
무엇이 더 중요한지를 충분히 검토해야 합니다'
따라서, (실수가 포함된) 회계계산에는 언어를 불문하고 decimal 을 많이 사용합니다
(한국 화폐 기준만 사용하시나요? 그렇다면, int64 로도 충분할 것입니다)
앞서 예제 코드를 double 대신 decimal 로 바꿔 봅시다
decimal a = (decimal) 11.22;
decimal b = (decimal)11.10 + (decimal)0.12;
bool result = (a == b);
Console.WriteLine(result.ToString());
Console.WriteLine("{0:e16}", a);
Console.WriteLine("{0:e16}", b);
결과입니다

값이 같다는 결과를 보여주죠..
이제, 이 글에서 제가 하고 싶은 본론입니다
decimal 을 사용하지 않고도 실수 연산의 결과가 보장(?)되어야 한다는 경우가 있을 것입니다
음.. 사실 이 표현은 정확하지 않죠. 부동소수점 연산 자체가 이미 정확하지 않은데 어떻게 연산의 결과를
보장하겠습니까?
그러면 표현을 다르게 해 보죠
부동소수점 실수를 사용하고도 허용하는 범위 내에서는 결과가 (오차가 없다는 것을) 보장해야 한다
이러면 말이 되죠. 이러한 것을 내결함성 허용이라 합니다
부동소수점 실수 연산에서 연산의 결과가 차이나는 것은 컴퓨터의 실수 표현에 따른 미세한 오차 때문입니다
즉 이러한 미세한 차이는 허용할 수 있다는 가정입니다. 대부분은 이러한 미세한 차이는 허용가능합니다
잘 생각해 보세요. 0.1%의 오차도 허용하지 않겠다.... 라고 한다면 부동소수점 사용하면 안됩니다
실수 연산이 돈 계산만 아니면 (경우에 따라서는 돈 계산이라 할지라도),
어느 정도의 오차는 허용가능한 경우가 대부분입니다
0.1%의 오차 허용이 수치로 와 닿지 않나요?
그러면 특정 소수점 자리 수 까지만 정확성을 보장하면 되나요?
그렇다면, 부동 소수점으로도 충분히 연산 가능합니다
아래 코드는 0.%의 오차를 허용하는 환경에서의 두 값 비교 입니다
double a = 11.22;
double b = 11.10 + 0.12;
double difference = a * 0.0001; //0.1% 오차는 허용함
bool result = Math.Abs(a - b) <= difference; // true 반환
부동소수점 연산 결과의 오차는 특정한 범위 내에서는 허용가능한 경우가 많습니다
즉 컴퓨터가 부동소수점을 표현하는 방식에시 기인한 오차 범위 수준 정도는 무시해도 된다는 거죠
예를 들어, 소수점 2자리 까지만 사용하는 환경에서
0.0000001 오차 때문에 double 대신 decimal 을 사용한다는 것은 좀 오버 아닐까요???
MS 고객지원 사이트에는 다음과 같은 글이 있습니다
'서로 같은지 확인하기 위해 두 개의 부동 소수점 값을 비교하지는 마십시오.
반드시" 같아야 하는 두 숫자 사이에도 항상 약간의 차이가 납니다.
그 대신 항상 숫자들이 거의 근사한 값인지 확인하십시오.
즉, 두 수의 차이가 아주 작은지 또는 무의미한지 확인하십시오'
다음의 MS 자료들을 찬찬히 읽어 보시길 권장 드립니다
http://support.microsoft.com/kb/42980/ko
http://support.microsoft.com/kb/125056/ko
http://support.microsoft.com/kb/69333/ko
http://msdn.microsoft.com/ko-kr/library/c151dt3s.aspx
'SW개발' 카테고리의 다른 글
| ASCII (249) | 2023.10.27 |
|---|---|
| 비트(bit) 단위 연산 (0) | 2023.10.27 |
| +- m * n의 e승 (1) | 2023.09.27 |
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=99
---
앞에서 부동 소수점 방식에 대해 간략히 알아 봤습니다. 보통 프로그래밍 언어에서 실수형 데이터를 저장하기 위해
두가지 데이터 타입을 둡니다. float 와 double 이지요..
float : 단정도 부동 소수 (32비트)
double : 배정도 부동 소수 (64비트)
데이터를 표현하는데 사용되는 비트수가 다르기 때문에 당연히 표현가능한 수의 범위가 달라집니다.
컴퓨터는 실수형 데이터를 표현하기 위해 할당되어진 비트들 중 특정 비트를 지수,가수,부호로 사용함으로써
실수를 표현합니다. 이 두 형식 모두 앞서 살펴본 (아래의)부동 소수 표현식으로 표현됩니다.
+- m * n의 e승
+- : 부호
m : 가수
n : 기수
e : 지수
아래의 그림은 배,단정도 부동소수 저장시 사용되어 지는 메모리 구조 입니다.
1) 단정도 부동 소수의 메모리 구조(32 비트 사용)

2) 배정도 부동 소수의 메모리 구조(64 비트 사용)

앞서, 우리는 위 표현식이 엄밀히 말하면 아래와 같다고 했습니다.
+- 1.m * 2의 e-127승
이유를 하나하나 살펴 봅니다.
[1] 기수는 2 이다
컴퓨터는 2진수를 사용하기 때문에 기수는 2가 되어 아래의 표현식으로 됩니다
+- m * 2의 e승
[2] 지수부는 excess 표현이 사용된다
지수부 역시 양수와 음수를 가져야 합니다.
10진수의 부동소수 표현에서 10의 지수 값으로 소수점의 위치가 변동 됨을 알 수 있습니다. 이는 2진수도 마찬가지
입니다. 즉, 지수부의 값이 - (마이너스) 가 되어야 할 필요가 있다는 말입니다. 그러나 지수부를 위한 메모리 공간에
는 별도의 부호 비트는 없습니다. 따라서 특별한 규칙을 만들어 마이너스를 표현하는데요...
이때 사용되는 것이 excess 표현입니다.
excess 표현은 지수부에서 나타낼 수 있는 최대 값을 반으로 나누어 그 값을 0 으로 보고
그것(0)보다 큰 값을 양수처럼, 작은값을 음수로 계산하는 것입니다.
(즉 최대값을 반으로 나눈 값을 기준으로 본다는 말이 됩니다)
한가지 예를 들어 보겠습니다.
단정도 부동소수인 float 에서 지수부를 위한 메모리 공간은 8비트 입니다.
8비트로 표현할 수 있는 최대 수는 11111111 이므로 10진수로 255 가 됩니다.
255 / 2 = 127.5 가 됩니다. 여기서 소수점 0.5는 버립니다.
즉 127을 0으로 취급합니다.
이때 지수부의 실제 값이 128이면 excess표현으로 인한 지수의 값은 1 이 되는 셈입니다
따라서 지수부의 값은 e-127 이 되느 것입니다.
+- m * 2의 e-127승
[3] 가수부는 특정 규칙을 사용하는 정규 표현을 사용한다
부동소수는 이미 알아본 바와 같이 다양한 형태로 표현될 수 있습니다.
10진수로 예를 들면 고정 소수 0.12 를 표현하기 위한 부동 소수는 아래와 같이 다양합니다.
0.12 = 0.12 * 10의 0승
0.12 = 12 * 10의 -2승
0.12 = 0.012 * 10의 1승
이와 같이 같은 수에 대한 표현방법이 다양하다면, 컴퓨터로 처리하기가 어려워 집니다. 따라서 특정한 표현방식
하나만 정해서 사용합니다. 위의 0.12 를 아래와 같이 하나의 표현 방식만 사용한다고 정해 둔다는 것입니다.
'소수점 이상은 0으로 하고, 소수점 이하 첫번째 자리는 0이 아닌 값으로 한다'
위의 규칙대로라면 0.12의 부동 소수 표현은 0.12 = 12 * 10의-2승 .. 이것만 가능 합니다.
이와 같이 특정 규칙을 정해 그 규칙대로만 표현하는 것을 정규 표현이라 합니다. 컴퓨터에서 2진수로 표현하는 부동소수 표현 방식에 이와 같은 규칙이 있습니다. '소수점 이상을 1로 고정한다' 라는 정규 표현을 사용합니다.
즉 반드시 정수부의 첫번째 자리는 1로 만들고 그 이상의 자리는 0으로 해주는 표현방법입니다.
소수점 이상을 1로 고정 하기 위해 2진수의 쉬프트 연산이 일어납니다. 또한 이렇게 고정한 1은 가수부의 표현
비트내에 포함시키지 않습니다. 정수부의 첫번째 자리는 반드시 1이라고 규칙을 정해 놓았기 때문에 별도의
비트가 필요치 않으며 가수부 비트내에 포함시키기 않음으로써 조금 더 넓은 범위의 수를 표현할 수 있게 됩니다.
(단정도 부동소수의 경우 23비트로 가수부를 표현하는데 첫번째 자리 1이 생략되었다고 할 수 있으므로 총 24비트
를 사용한다고 할 수 있을 것입니다)

아래는 단정도 부동 소수에서 가수부의 정규 표현을 사용하여 표현한 것입니다.
1011.0011 <- 원래의 숫자
0001.0110011 <- 정수부의 첫번째 자리가 1이 되도록 오른쪽 쉬프트
0001.01100110000000000000000 <- 소수점 이하를 23비트로 만듦
01100110000000000000000 <- 소수점 이하만 뽑아 정규 표현을 완료
Example>>
2진수로 표현된 실수(단정도 부동소수)가 아래와 같다고 할때 10진수로 변환하면...?
0 01111110 10000000000000000000
부호 지수부 가수부
1) 부호비트가 0 이므로 양수입니다.
2) 지수부의 값이 126 이므로 (127 - 126) = -1 , 즉 2의 -1 승 , 0.5가 됩니다.
3) 가수부의 소수점 이상 첫번째 자리가 1이므로
위의 가수부의 값은 1.10000000000000000000000 이 됩니다.
즉 10진수로 1.5가 됩니다.
결론)
+- m * 2의 e승
이 표현식에 대입해 보면 + 1.5 * 0.5 = 0.75 가 됩니다
'SW개발' 카테고리의 다른 글
| 비트(bit) 단위 연산 (0) | 2023.10.27 |
|---|---|
| 실수 연산, 어떻게 하시나요??? (3) | 2023.09.27 |
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=98
---
컴퓨터가 정수를 표현하는 방식과 실수를 표현하는 방식은 크게 다릅니다.
실수 표현 방식을 이해하기 위해 아래와 같은 가정으로 출발하여 컴퓨터가 실수 표현을 하는 방식에 대해 알아
봅니다. 한가지 예를 들겠습니다.
만일 2바이트의 메모리로 실수를 표현한다고 가정할때, 가장 쉽게 생각해서 반을 나누어 1바이트에는 소수점
이상의 값을, 또 다른 1바이트에는 소수점 이하의 값을 저장한다고 칩시다. 아래와 같이 표현될 것입니다.
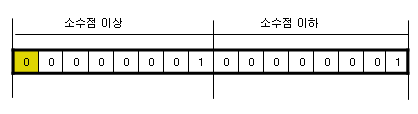
위와 같이 표현한다면 소수점 이상이 00000001 이므로 10진수 1이 되며, 소수점 이하는 00000001 이 되어 10진수
1이 되므로 +1.1 이 된다고 해석될 것입니다.
아주 심플하면서도 이해하기 쉽습니다. 그러나 컴퓨터는 일반적인 실수 표현을 위와 같은 방식을 채택하지는
않았습니다. 이유가 뭘까요?? (쉬운데 기냥 저렇게 하지-.-;)
이유는 바로 데이터의 표현한계입니다.
위와 같이 실수를 표현한다면 2바이트로 표현할 수 있는 실수의 범위는 아주 작습니다. 4바이트든, 8바이트든
실수 표현 범위의 한계를 가질 것입니다. 그렇다고 해서 아주 넓은 범위의 실수를 표현하기 위해 메모리를 확
늘려 데이터를 저장한다고 하면 해결책이 될까요?? 도대체 얼마나 많은 메모리를 요구해야 현실세계의 실수를
모두 표현 할 수 있을까요??
그래서 컴퓨터는 적은 수의 비트 수를 가지고 넓은 범위의 실수를 표현하기 위해서 하나의 식을 만들었습니다.
+- m * n의 e승
+- : 부호
m : 가수
n : 기수
e : 지수
위와 같은 식을 미리 정해 놓고 일부 비트는 가수로 일부 비트는 지수의 값을 정하는데 사용하여 실수를 표현합니다.
위의 식을 도입하여 적은 비트로 넓은 실수 범위를 표현가능 하다는 장점을 얻었지만 실수표현에서의 오차를 허용 할 수 밖에 없는 단점도 가지게 되었습니다. 앞서 살펴본 실수표현의 오차는 실제로 위의 식으로 기인하는 것입니다.
위와 같이 실수에서 소수점의 위치를 고정 시키는 것이 아니라 지수승에 따라 소수점이 움직일 수 있는 것을
부동 소수점 표현 방식이라고 합니다. (부동의 '부' 는 아닐 '부' 가 아닙니다. 둥둥 떠 다니는 '부' 입니다 ^^;)
위의 부동 소수의 표현 방식은 정확히 말해 아래와 같이 표현됩니다.
+- 1.m * 2의 e-127 승
즉 2진수에서 기수는 2이며 가수부와 정규표현과 지수부의 excess 표현이 사용된 것입니다.
이에 관해 다음에 자세히 알아 봅니다
참고>
우리가 사용하는 10진수에서도 고정,부동 소수점 표현방식으로 소수점을 표현을 달리 할 수 있습니다.
ex> 0.12 의 소수점을 가진 실수의 표현은 아래와 같이 다양합니다.
1)0.12 = 0.12 * 10의0승
2)0.12 = 12 * 10의-2승
3)0.12 = 0.012 * 10의1승
즉 고정소수점인 0.12 는 10의 지수승의 변화를 주어 다양한 부동 소수점 방식으로 표현 될 수 있습니다
'SW개발' 카테고리의 다른 글
| 실수 연산, 어떻게 하시나요??? (3) | 2023.09.27 |
|---|---|
| +- m * n의 e승 (1) | 2023.09.27 |
| 0.1 을 100 번 더해도 10이 되지 않는다? (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=97
---
너무나도 유명한 문구가 아닌가 싶습니다.
기초 C언어 공부할때나 프로그래밍 원리 같은 공부할때 꼭 등장하는 말입니다. 저도 그 말을 인용해 봤습니다.
이 말은 컴퓨터의 실수 표현 방식과 그에 따른 오차에 관한 말인데요.. 실제로 실수형 데이터의 연산에는 오차가
발생합니다. (직접해보세요.. 0.1 , 100 번 더하기)
이미 우리는 앞에 2진수로 표현된 수를 10진수로 변환하는 방법을 알고 있습니다. 그러면 2진수로 표현된 소수를
10진수로 변환하는 방법은요??? ... 마찬가지 입니다.
EX>2진수 1.01 을 10진수로 만들어 보겠습니다.
(2진수) 1.01 => 1*2의0승 + 0*2의-1승 + 1*2의-2승 = 1 + 0 + 0.25 = 1.25 (10진수)
이렇듯 2진수를 10진수로 표현할 때는 소수점을 기점으로 2의 (+,-)승을 해나가면 됩니다.
그렇다면 10진수 소수인 0.1 은 2진수로 어떻게 표현될까요???
소수점 이하 자리는 2의 마이너스 승이므로 2의 -1 승부터 차례로 해 보겠습니다
2의-1승 = 0.5 , 2의-2승 = 0.25 , 2의-3승 = 0.125 , 2의-4승 = 0.0625 ………
0.125 에서 바로 0.0625 로 넘어가 버렸습니다. 0.1은 나오지도 않았는데 말이죠..
물론 비트 자릿수를 늘려 이 들 숫자의 조합으로 0.1 에 가까운 수를 찾을 수는 있습니다만, 0.1이 아닌 근사값이
됩니다. 위의 산술과정은 비트자릿수를 하나씩 늘려서 0보다 큰 제일 작은 수를 나타낸 것인데요..
이런 방식이 아니더라도 소수점 이하 4비트를 가지는 메모리에서 표현되는 수를 다시 한번 보겠습니다.
소수점 이하 4비트를 가지는 2진수의 제일 작은 수 : 0.0000 => 10진수 0
소수점 이하 4비트를 가지는 2진수의 그 다음 작은 수 : 0.0001 => 10진수 0.0625
즉, 이 메모리로는 10진수 0과 0.0625 사이의 값은 표현할 수가 없습니다.
비트 수를 더 늘리면 더 좁은 간격의 수가 나올 수 는 있겠습니다만..
이렇듯 컴퓨터는 10진수 실수를 표현하는데 오차를 가집니다.
10진수에 해당하는 실수 값에 근사값을 나타낼 수 있을 뿐이지요..
결론적으로 0.1 이라는 값을 가지는 변수를 선언하면 그 변수에는 실제 0.1이 들어가는 것이 아니라 0.1의 근사값이
저장됩니다. 즉, 0.1의 근사값을 100번 더해봤지 10이 될리 없는 것입니다.
실제로 10진수 0.1을 2진수로 변환하면 0.00011001100....... (이하 1100 반복)이 됩니다
이런 수를 수학에서는 순환소수라 합니다.
대표적인 순환소수는 1/3 이 있습니다. 1/3 을 소수로 표현하면 0.33333.....(이하 3반복) 이 됩니다
참고>>
위의 내용은 문제를 간단하게 표현하기 위해 그리고 오차가 나는 이유를 이해하기 위해 2진수 소수 표현방식을 나타 냈습니다. 그러나 실제로 컴퓨터는 실수 표현을 단순히 소수점을 가진 2진수로 표현하지는 않습니다.
미리 말씀드리자면 일정한 식을 가지고 비트를 각 영역별로 나누어 저장,표현합니다. 이에 대해선 다음에 알아봅니다
'SW개발' 카테고리의 다른 글
| +- m * n의 e승 (1) | 2023.09.27 |
|---|---|
| 실수 데이터의 표현 방식 - 부동소수점 방식 (2) | 2023.09.27 |
| 정수 데이터의 표현 방식 (2) | 2023.09.27 |
| 2진수 <-> 8 진수, 16 진수 변환 (2) | 2023.09.27 |
| n 진수? 진수 변환 ! (0) | 2023.09.27 |


