이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다. 원본 글은 2008년 5월에 작성되었습니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두... 그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=106
『 다차원 배열의 인덱싱 』
앞서 arr[3] 과 같은 1차원 배열에서의 인덱싱 기법을 알아 보았다.
만일 arr[2][2] 와 같은 2차원 배열이라면 어떤 메커니즘으로 각 요소를 찾아 낼 수 있을 것인가?
눈치 챘을 수도 있지만 원리는 1차원 배열과 완전 동일하다.
1차원 배열과 마찬가지로 아래의 내용이 핵심이다.
“배열은 연속된 메모리 공간에 순차적으로 저장된다”
이것은 2차원이든 3차원이든 모두 동일한 원칙이다.
만일, arr[2][2] 라는 2차원 배열이 있다면 2행 2열의 배열로써 편의상 아래와 같은 표현으로 인식했다.
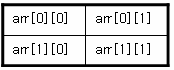
그러나 실제 메모리에서는 연속된 메모리 공간에 값을 저장하게 된다. 아래 그림처럼..

즉, 다차원 배열 역시 연속된 공간에 순차적으로 저장되는 자료구조이기 때문에 1차원 배열과
유사한(사실은 동일한) 포인터 연산으로 각 요소에 접근할 수 있게 되는 것이다.
그럼 샘플 하나를 보고 이해해 보자.
arr[2][2] 로 정의된 배열의 arr[1][1] 의 요소를 찾는 연산은 아래와 같다.
a [1][1] = *( arr + ((1 * 2) * 4byte) + (1 * 4byte) ) = *(arr + 8 + 4) = *(arr + 12)
배열의 첫 요소를 가리키는 arr 상수 포인터가 0x20을 가리키므로 arr 에서 12 byte 이동한 메모리인 0x32 를 포인팅하게 되는 것이다.
위의 식이 복잡해 보인다면 int 형 배열이기 때문에 자동으로 곱해 지는 4byte 를 생략해서 생각해 보자.
a[1][1] = *(arr + (1 * 2) + 1 ) = *(arr + 2 + 1) = *(arr + 3) 가 되어 3칸을 이동하게 되는 것이다 (int 형 메모리의 한 칸은 4byte 이므로 3칸이라 함은 12byte 이다)
1차원 배열과 조금 다른 점은 배열의 ‘열 정보’ 즉 열 값을 곱해 주는 것이다.
Arr[2][2] 의 열 값은 2이다
메모리 구조를 보면 당연한 것이다
행과 열을 가진 배열은 순차적으로 행 단위로 저장이 되기 때문에 열의 숫자를 곱해 줘야 그만큼 메모리
이동이 가능한 것이다 ( (0,0) -> (0,1) -> (1,0) -> (1,1) ... )
아래 그림은 내부적으로 곱해 지는 4byte 를 제외한 상태에서 쌍으로 색깔로 매핑 시킨 것이다.

참고로 다차원 배열을 포인터로 표현해 보자.
앞서 배열은 포인터이므로, 1차원 배열은 int *p = arr 이 로 표현된다고 하였다.
다차원 배열은 다음과 같이 표현되어야 배열과 포인터가 서로 같다고 할 수 있다
int (*p)[열];
즉, int arr[2][2] 일 경우
int (*p)[2] = arr 이 성립되는 것이다
이과 같이 정의된 포인터 p 를 배열 포인터라 한다
주의> 배열 포인터와 포인터 배열을 혼동하지 말기 바란다.
포인터 배열은 int *p[2] = {&a, &b} 와 같이 포인터 자체를 여러 개 가진 것을 말하는 것이다
(괄호의 유/무가 이런 엄청난 차이를 보이네요 ^^; )
이로써 다차원 배열의 인덱싱 메커니즘을 알아 보았다.
이것은 2차원뿐만 아니라 3차원 이상에서도 동일한 메커니즘이다.
'SW개발' 카테고리의 다른 글
| SBCS, MBCS, WBCS (0) | 2023.10.31 |
|---|---|
| 이런... 계집 녀(女) (6) | 2023.10.31 |
| 배열 인덱싱의 메커니즘(arr[i] == *(arr+i)) (2) | 2023.10.27 |
| 배열과 포인터(Pointer) 의 상관관계 (2) | 2023.10.27 |
| 리터럴(Literal) 상수 (1) | 2023.10.27 |


