실수 데이터의 표현 방식 - 부동소수점 방식
이 글은 제가 과거에 운영했던 사이트인 http://dotnet.mkexdev.net 의 글을 옮겨온 것입니다.
그 전에 운영했었던 사이트(mkex.pe.kr)은 흔적도 없이 사라 졌습니다. 그속의 글들도 모두...
그래서 이 사이트도 사라지기 전에 옮기고 싶은 글을 조금씩 이 블로그로 이동시키려 합니다.
(원본글) http://dotnet.mkexdev.net/Article/Content.aspx?parentCategoryID=2&categoryID=9&ID=98
---
컴퓨터가 정수를 표현하는 방식과 실수를 표현하는 방식은 크게 다릅니다.
실수 표현 방식을 이해하기 위해 아래와 같은 가정으로 출발하여 컴퓨터가 실수 표현을 하는 방식에 대해 알아
봅니다. 한가지 예를 들겠습니다.
만일 2바이트의 메모리로 실수를 표현한다고 가정할때, 가장 쉽게 생각해서 반을 나누어 1바이트에는 소수점
이상의 값을, 또 다른 1바이트에는 소수점 이하의 값을 저장한다고 칩시다. 아래와 같이 표현될 것입니다.
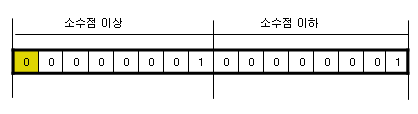
위와 같이 표현한다면 소수점 이상이 00000001 이므로 10진수 1이 되며, 소수점 이하는 00000001 이 되어 10진수
1이 되므로 +1.1 이 된다고 해석될 것입니다.
아주 심플하면서도 이해하기 쉽습니다. 그러나 컴퓨터는 일반적인 실수 표현을 위와 같은 방식을 채택하지는
않았습니다. 이유가 뭘까요?? (쉬운데 기냥 저렇게 하지-.-;)
이유는 바로 데이터의 표현한계입니다.
위와 같이 실수를 표현한다면 2바이트로 표현할 수 있는 실수의 범위는 아주 작습니다. 4바이트든, 8바이트든
실수 표현 범위의 한계를 가질 것입니다. 그렇다고 해서 아주 넓은 범위의 실수를 표현하기 위해 메모리를 확
늘려 데이터를 저장한다고 하면 해결책이 될까요?? 도대체 얼마나 많은 메모리를 요구해야 현실세계의 실수를
모두 표현 할 수 있을까요??
그래서 컴퓨터는 적은 수의 비트 수를 가지고 넓은 범위의 실수를 표현하기 위해서 하나의 식을 만들었습니다.
+- m * n의 e승
+- : 부호
m : 가수
n : 기수
e : 지수
위와 같은 식을 미리 정해 놓고 일부 비트는 가수로 일부 비트는 지수의 값을 정하는데 사용하여 실수를 표현합니다.
위의 식을 도입하여 적은 비트로 넓은 실수 범위를 표현가능 하다는 장점을 얻었지만 실수표현에서의 오차를 허용 할 수 밖에 없는 단점도 가지게 되었습니다. 앞서 살펴본 실수표현의 오차는 실제로 위의 식으로 기인하는 것입니다.
위와 같이 실수에서 소수점의 위치를 고정 시키는 것이 아니라 지수승에 따라 소수점이 움직일 수 있는 것을
부동 소수점 표현 방식이라고 합니다. (부동의 '부' 는 아닐 '부' 가 아닙니다. 둥둥 떠 다니는 '부' 입니다 ^^;)
위의 부동 소수의 표현 방식은 정확히 말해 아래와 같이 표현됩니다.
+- 1.m * 2의 e-127 승
즉 2진수에서 기수는 2이며 가수부와 정규표현과 지수부의 excess 표현이 사용된 것입니다.
이에 관해 다음에 자세히 알아 봅니다
참고>
우리가 사용하는 10진수에서도 고정,부동 소수점 표현방식으로 소수점을 표현을 달리 할 수 있습니다.
ex> 0.12 의 소수점을 가진 실수의 표현은 아래와 같이 다양합니다.
1)0.12 = 0.12 * 10의0승
2)0.12 = 12 * 10의-2승
3)0.12 = 0.012 * 10의1승
즉 고정소수점인 0.12 는 10의 지수승의 변화를 주어 다양한 부동 소수점 방식으로 표현 될 수 있습니다